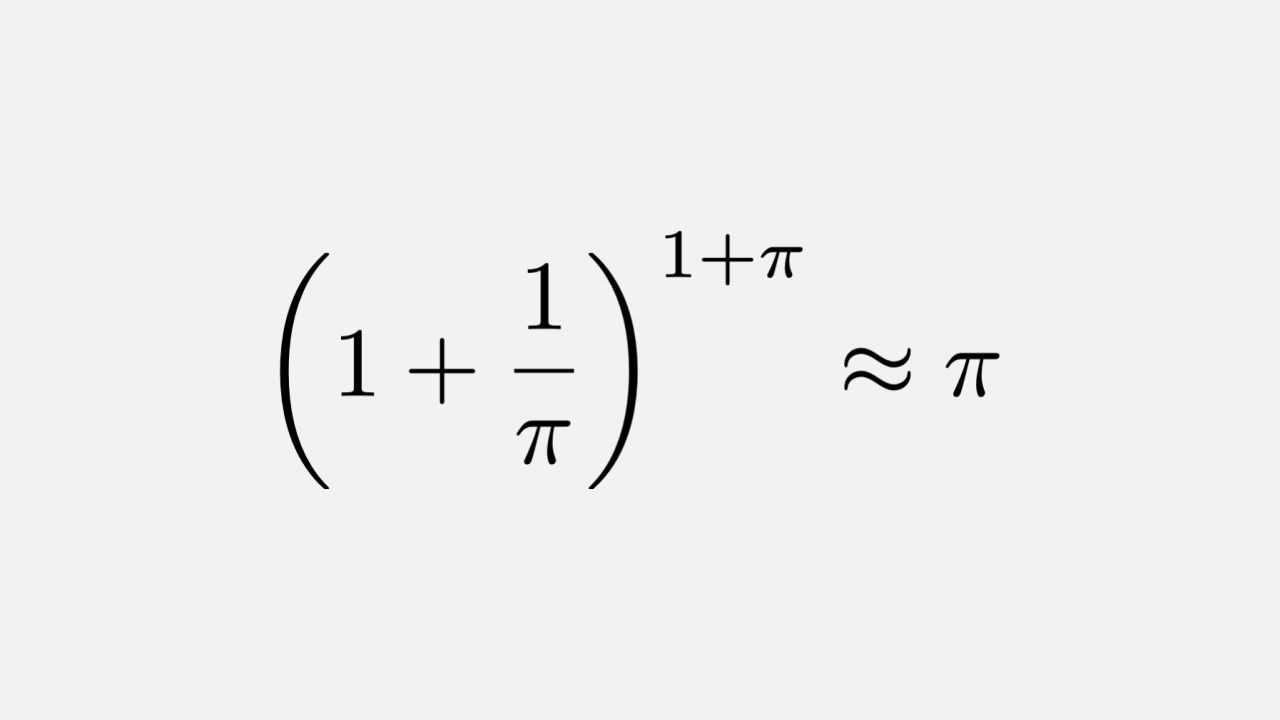Как посчитать и проверить равенство?

Question

[Михаил]

Всем привет!
Кто-нибудь знает, как доказать что это равенство (предел?) равно только для ПИ?
И только ли для ПИ это верно, есть ли другие значения при котором равенство выполняется?
Это оносится к т.н. "классичсеским пределам" или в какую категорию это можно отнести?
Какая математическая база за этим стоит?



Заранее спасибо за ответы!
P.S. я математику совсем забыл, последний раз ей на таком уровне занимался больше 20-ти лет назад наверно... ничего не помню уже

Comments

[AVKor]

Лентюй, Который из них?

[U235U235]

https://www.wolframalpha.com/input/?i=%281%2B1%2Fx...

Answer 1

[Wataru]

Возьмите функцию f(x)=(1+1/x)^(1+x)-x.

Через матан (взять производную, убедиться, что она всегда отрицательна. Подсчитать значение f(x) при x=1) можно убедится, что у функции нет корней, кроме одного на отрезке (1, +inf), ведь она всегда убывает и для единицы она положительна.

Теперь мы знаем, что только одно число удовлетворяет этому уравнению.

Судя по всему, корень не пи: https://www.wolframalpha.com/input/?i=%281+%2B+1%2...

То, что он где-то там можно понять, если подсчитать функцию в точках 3.1, 3.2, 3.3 - между двумя, где функция меняет знак, и лежит корень.