Человек сразу выделяет три направления (см. рисунок ниже). Поэтому можно выбрать косоугольную систему координа (на рисунке: красные линии — горизонтальное направление и наклонное) с углом 60°. Тогда вдоль красных направление соотв. координата будет возрастать, а вдоль голубого — одновременно две. Расстояния между центрами будет вычислятся по формуле
Где Г — матрица Грамма этой косоугольной системы:
Это в случае, когда расстояния между центрами соседей 1.
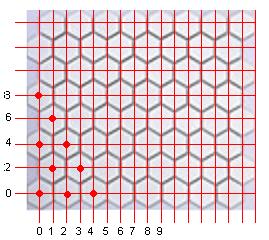
Использовать стандартную двумерную декартову систему координат. Единственная особенность, есть запрещенные положения.
Плюсы
1) Это понятно и естественно. Даже запрещенные состояния есть в нашем мире (При́нцип Па́ули).
2) Расстояние вычисляется по формуле = sqrt( (x1-x0) ^ 2 + (y1-y0) ^ 2 )
3) Если x1!=x0 и y1!=y0, значит это различные координаты (в отличии от трехкомпонентной системы)
Если под расстоянием Вы понимаете минимальное число переходов между двумя смежными гексами, образующих непрерывный путь от одного гекса к другому, то всё очень просто. Ось абсцисс проводим обычным образом, горизонтально, ось ординат — под углом 60° к ней. Расстояние между гексами (x1, y1) и (x2, y2) вычисляем следующим образом:
обозначим для простоты δx = x2 − x1 и δy = y2 − y1;
при δy ≥ 0 расстояние ρ ((x1, y1), (x2, y2)) =
δx + δy, если δx > 0;
δy, если − δy ≤ δx ≤ 0;
− δx, если δx ≤ − δy.
При δy < 0 переставляем точки местами или, что то же самое, переобозначаем δx = − δx и δy = − δy, после чего применяем ту же формулу.
В подобном вопросе «приближение к человеческому варианту» отражается на скорости работы.
Если Вы не извращенец, то будете использовать какой-нибудь алгоритм поиска в ширину. А его, как не странно, оптимально применять над одномерным представлением.
для моей игры на Canvas тоже рисовал похожее поле :) с той лишь разницей, что у меня оно повёрнуто на 90 градусов. система координат 2-мерная. Х — как обычно, Y идёт змейкой. чтобы с этим нормально работать приходится Y разделять ещё на чётные и нечётные, но это плата за шестигранники. чтобы определить, куда нажали, пришлось вспомнить тригонометрию, но там всё более-менее просто. самое главное — ничего не забыть :)
