Как решить олимпиадную задачу о трапеции?

Question

[Александр]

Меньшее основание равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равно 4.0. Найдите большее основание трапеции, если ее площадь равна 110.0. Формат ответа: приближённый с точностью до 0.01.
Пусть BC - меньшее основании. Далее посчитал, что BO=CO = корень 8, а также AOD - равнобедренный. А как дальше не знаю.

Comments

[mayton2019]

А в каких случаях диагонали перпендикулярны? В квадрате разве что?

[Александр]

mayton2019, а ведь правда... спасибо.

[Rsa97]

mayton2019, Не только в квадрате. Возьмите одно из оснований трапеции, постройте на нём равнобедренный треугольник с прямым углом в вершине. Продолжите стороны этого треугольника за вершину. Любая линия, соединяющая продолженные стороны и параллельная первому основанию даст второе основание.

[mayton2019]

Rsa97, хм...

[Александр]

Тоже про это думал.

Answer 1

[Rsa97]

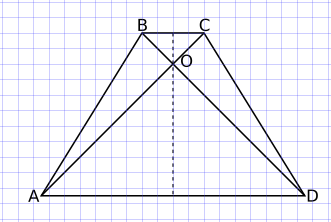
Треугольники BOC и AOD прямоугольные (из условия задачи), равнобедренные (треугольники ABC и BCD, ACD и ABD попарно равные, значит и высоты у них равные) и пропорциональные. Длины оснований будут, соответственно, BC и AD, высоты BC/2 и AD/2. Из пропорциональности получаем AD = k*BC.
Значит площадь трапеции
S = (BC + AD) * (BC/2 + AD/2) / 2 = (BC + k*BC) * (BC/2 + k*BC/2) / 2 =
= BC²(1 + k)²/4 = 4(1 + k)² = 110
(1 + k)² = 27.5
1 + k = 5.244
k = 4.244
AD = 4.24 * 4 = 16.976

Comments

[Rsa97]

Zzzz9, Площадь трапеции - полусумма оснований, умноженная на высоту трапеции.

[Rsa97]

Zzzz9, O - точка пересечения диагоналей.

[Rsa97]

Zzzz9, Если AD = 21.354, то площадь трапеции
S = (BC + AD) * (BC / 2 + AD / 2) / 2 = (4 + 21.354) * (2 + 10.677) / 2 = 160.706
Так что это ваш результат неверен.

[Zzzz9]

Извини, картинку я не видел.

[Rsa97]

Zzzz9, Треугольники BCO и ADO - равнобедренные прямоугольные. В таких треугольниках высота равняется половине основания. Сумма высот треугольников даёт высоту трапеции.

[Zzzz9]

Автор не показал чертеж, я не правильно построил. Извини.

Answer 2

[Wataru]

Тут надо на листочке нарисовать трапецию. Чуть чуть школьной геометрии и вы получите формулу, которую надо запрограмировать.

Совет: обозначте за x длину диагонали от точки пересечения к углу короткого основания. За y обозначьте оставшейся кусок диагонали (к большему основанию). У вас там 4 прямоугольных треугольнка образуются со сторнами xx, xy, yx, yy. Сумма их площадей - 110. Диагональ треугольника xx тоже дана (это короткое основание - 4). Искомое оснавание - диагональ треугольника yy (по теореме пифагора получается sqrt(2)*y).

Составьте 2 уравнения, решите их, формулу запрограммируйте.