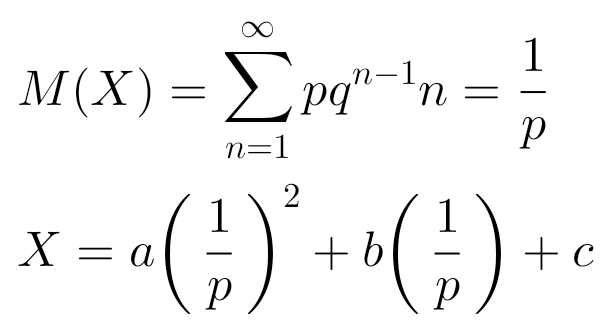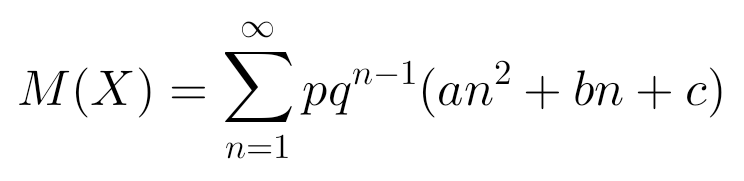я могу найти средний номер и воспользоваться им для нахождения величины X, будет ли она средней?
Ни в коем случае!
Сформулирую правило:
Пусть у меня есть некая случайная величина R. И есть функция T(R).
Если функция T(R) является линейной, т.е. T(R)=a*R+b (где a и b - константы), то в этом случае M(T(R))=T(M(R)) ; т.е. тут можно усреднить сначала аргумент функции, потом взять функцию от среднего значения аргумента.
Если функция T(R) является нелинейной, и её вторая производная положительна, то M(T(R))>T(M(R)) .
Для примера можете рассмотреть T(R)=R
^2 и R, симметрично расположенный вокруг нуля. Можно даже взять R, который с равной вероятностью распределён между значениями "один" и "минус один", так совсем просто. В силу симметрии M(R)=0, а вот M(T(R)) явно будет больше нуля.