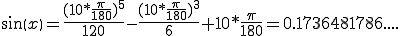Как найти синус 10 градусов?

Question

[xverizex]

Я знаю что есть формула синуса это катет на гипотенузу, но эту ли формулу надо использовать чтобы вычислить значение.

Можно получить радианы 10 градусов, это pi / 18, но как это с синусом вычислить, я не могу понять что на что делить или умножать.

Comments

[vvs_zel]

sin(pi/18) является одним из трёх корней уравнения третий степени:
X^3 - 0.75*X + 0.125 = 0.
Все три корня действительные. Но вычисление по формуле Карно уводит в комплексную область. В конце мнимые части исчезнут. Но разбираться с этим не подарок.

[vvs_zel]

[vvs_zel]

[vvs_zel]

________k1 = 0.766 044 443 118 978 035 202...
sin(pi/18) = 0.173 648 177 666 930 348 851...

Answer 1

[Griboks]

Если надо просто вычислить, то калькулятор в помощь.
Если самому и без оценки, то разложи синус в ряд и посчитай столько членов, какая точность нужна.

Answer 2

[Сергей Соколов]

Приближенные значения обычно смотрят в таблицах или получают в калькуляторах.

Ещё есть такая формула (ряды Тейлора):
sin(x) ~= x⁵/5! + x³/3! + x
где x в радианах:


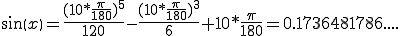
Если стоит задача именно без техники примерно найти sin(10°) можно воспользоваться бумагой, карандашом, линейкой и циркулем. sin() угла в прямоугольном треугольнике это отношение противолежащего катета к гипотенузе. Если нарисовать окружность радиуса 1, то sin() будет равен самой длине противолежащего катета.

Нарисуйте окружность радиусом, скажем, 10 см (будем считать 1 = 10см). Отмерьте угол в 1/18 полукруга (прямой угол разделить на три части и ещё раз на три). Опустите перпендикуляр из точки на окружности на горизонтальную ось. Его длина, делёная на 10см будет значением синуса.

Comments

[xverizex]

А чем тогда радианы от синуса отличаются, если ответ почти такой же?

[Сергей Соколов]

xverizex: радианы, как и градусы – просто мера угла. Синус – отношение катета, который непропорционально, а иначе, сложнее, зависит от угла, к гипотенузе.

Если равномерно менять угол, как секундная стрелка, то что радианы, что градусы будут меняться равномерно. А sin() такого угла при этом изменяется совсем не равномерно: то быстрее, то медленнее.

[xverizex]

А всё, увидел формулу.

[Сергей Соколов]

xverizex: анимация, красная штука по длине равна синусу угла, т.к. радиус = 1

[xverizex]

Сергей Соколов: Я нашёл формулу pi * угол / 180. Или она подходит только для малых углов?

[xverizex]

Этим я могу найти синус приблизительный.

Answer 3

[ivodopyanov]

Воспользуйтесь формулами синусов и косинусов суммы и приведите sin3X к f(sinX), а потом решите полученное уравнение

Answer 4

[7ett]

Для этого есть таблица Брадиса

Answer 5

[pantoriy]

Синус 30 гр = 0.5 далее через формулу тройного угла легко найти точный ответ. Никакие ряды не надо, известен точный результат в радикалах. А да, получится уравнение 3-ей степени, которое вам придётся решить. Но ничё, оно решается, по формулам Кардано. Какой сейчас сказать не могу, не помню формулу тройного угла... поищите в гугле... Кстати Тейлор плохой вариант. его базис неортогонален в функ пространстве. Поэтому ошибки начинают расти при увеличении числа членов. Синус собственно это вектор в бесконечномерном функциональном пространстве. Мы ищем его координаты. Для тейлора они известны и для Чебышева тоже. Уже всё давно подсчитано и не только ждя этих двух базисов. Но для синуса, периодической ограниченной фунции они не годятся. Но увеличение числа членов по разложению по Чебышеву уже стабильно повышает точность в отличие от Тейлора. Было бы веселее посчитать синус 6 градусов в радикалах... Хе-хе...

Answer 6

[mrbus]

По формуле Кардано получается неприводимый случай, когда вещественный корень выражается в комплексных радикалах, но не выражается в вещественных.

Answer 7

[MaxGlock]

Разумеется, есть идея, как писали выше, по формуле синуса тройного угла расписать синус 30 градусов и решать кубическое уравнение по формуле Кардано. И я попробовал это сделать. В этой формуле есть коэффициент Q, который определяет количество корней уравнения. Для получившегося уравнения (а именно 3x - 4x^3 = 1/2, где x - синус 10 градусов) Q меньше нуля, следовательно у нас три действительных корня. Казалось бы, всё хорошо, но эти корни получаются из комплексных чисел, а до этого вам из этих чисел нужно кубический корень извлечь, что делается по второй формуле Муавра, в свою очередь которая основыается на тригонометрическом представлении комплексных чисел. И в итоге у вас синус 10 градусов равен... синусу 10 градусов... Такие дела