Как найти координаты точки?

Question

[BadCats]

Дан отрезок и даны его координаты X1,Y1,0 - и его длина как найти координаты X2,Y2,0 ?
угол 90, 0 это Z. Эта задача для плоскости.
Задача у меня возникла в прямоугольном треугольнике, где известны координаты вершин, а та прямая о которой я говорю - это один из катетов
Просто уточню - также известны длины второго катета, ну и соответственно гипотенузы. И известны координаты катета(там где угол 90 - у основания) и известны координаты гипотенузы(которые у осинования). мне нужны координаты второго катета(которые против основания - на той же прямой, что образует 90).

Comments

[Сергей Соколов]

Не понятно, про какой отрезок идёт речь – это один из катетов или гипотенуза? Нарисуйте, пожалуйста, треугольник, обозначьте вершины, и укажите, что известно в задаче. Катет – это отрезок, а не точка. Перепишите вопрос.

Answer 1

[Сергей Соколов]

Перечитав ваш вопрос раз 5, вроде бы уловил его смысл. Как я понял, есть прямоугольный треугольник ABC (В – прямой угол). Известны длины всех сторон, координаты на плоскости вершин B и C. Надо найти координаты вершины A:

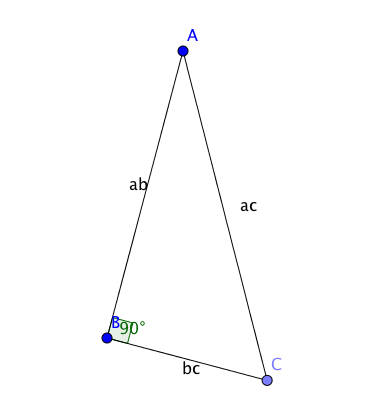
При таких условиях задача имеет два решения: точка с одной или с другой стороны от прямой BC (на рисунке – сверху или снизу, под BC)

Надо взять вектор BC, повернуть его на 90° (в одну или в другую сторону), и длину разделить на bc и умножить на ab:

x = Bx - ab * (Cy - By) / bc
y = By + ab * (Cx - Bx) / bc
// в другую сторону:
x = Bx + ab * (Cy - By) / bc
y = By - ab * (Cx - Bx) / bc

Answer 2

[Mercury13]

Я плохо понял, что надо сделать. Но попробую.
1. Переведи известный катет в вектор: (X3−X1, Y3−Y1).
2. Поверни его на 90° в нужную сторону. Например, x'=y, y'=−x.
3. Приведи к нужной длине (теорема Пифагора). Получился вектор-катет.
4. Прибавив вектор-катет к вершине (X1, Y1), получаем второй конец.