f(1, 1) = 100
f(1, 95) = 1.05
f = ?x - x1 y - y1
------- = -------
x2 - x1 y2 - y198.95 * x + 94 * y = 9498.95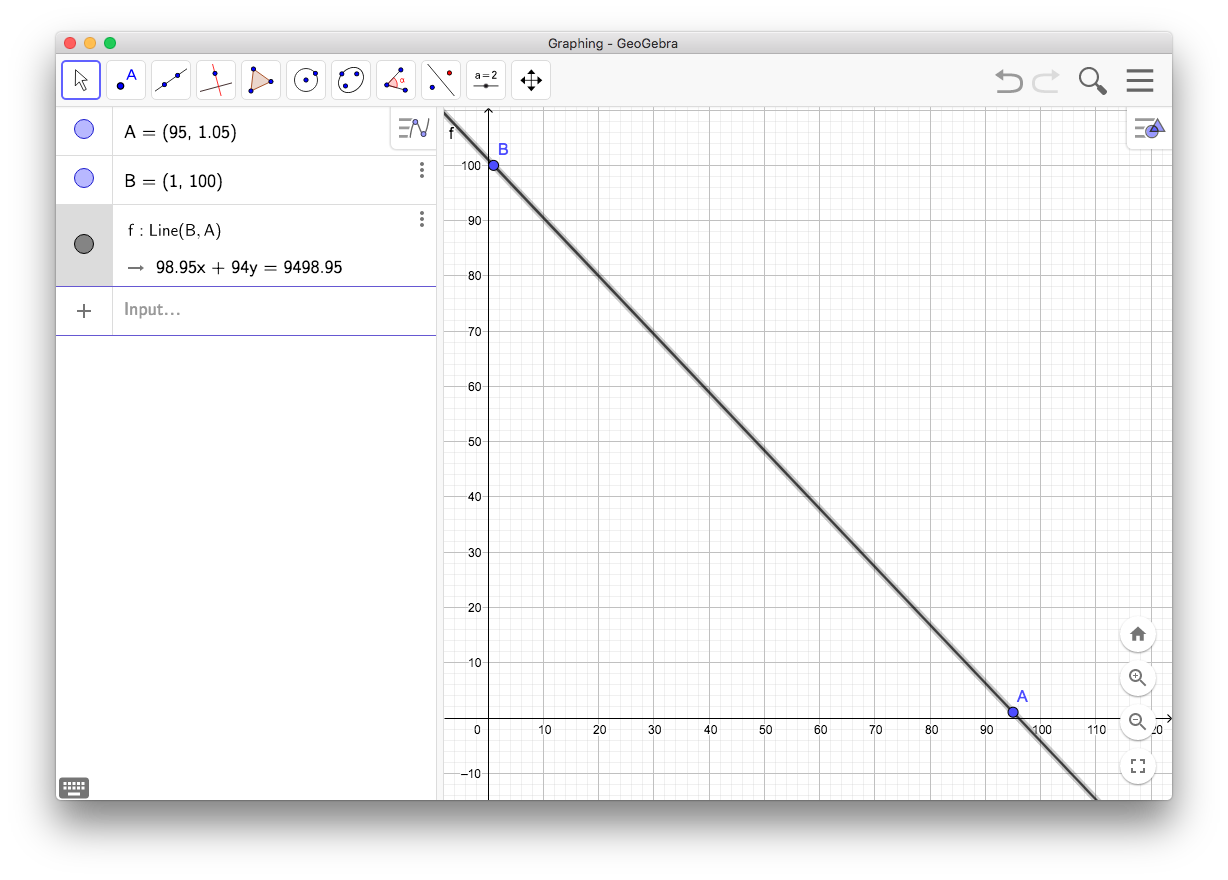
(|x| + x) / 2(|x| - x) / 2z > 0, вторая для z < 0. Параметр z тут только переключает части и более никак не участвует в результате. Если идея понятна, сможете модицифировать как вам удобнее.f(x,z) = ((|z| + z) / 2) * |x| + (|z| - z) / 2) * xx = a * cos(t)
y = b * sin(t)
0 ≤ t ≤ 2π
где a, b − полуоси эллипса, t − параметр.t: (sin^2 + cos^2) = 1a как функцию b при известных (x, y).a = f(b)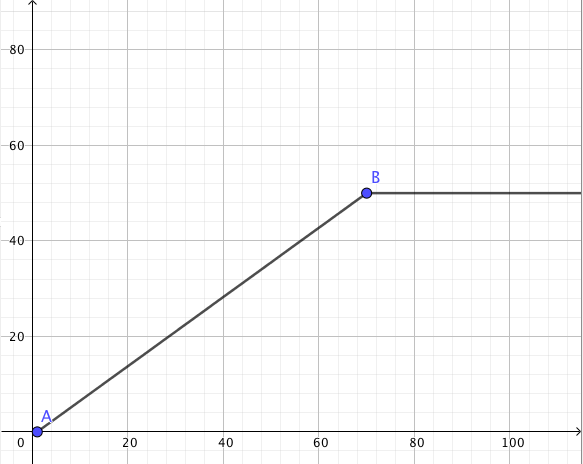
y = 1 / (e^x + 1)y = 50 / (ℯ^(5 - x / 8) + 1)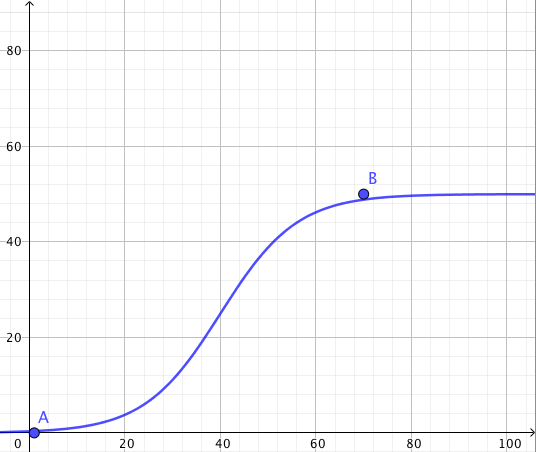
$ipsa3 так:$result = $ipsa3 * ((100 / 100) * $ipsa3);
// или просто
$result = $ipsa3 * $ipsa3;$percent = 100; // сколько процентов
$result = $ipsa3 * (($percent / 100) * $ipsa3);что-то * 0.5$ipsa3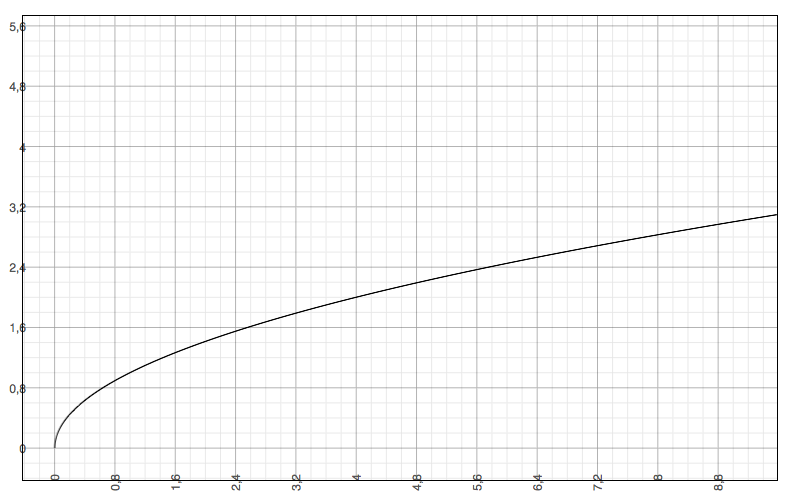
X = 0.7 * Y Что здесь сложного? Найдо найти все пары (X, Y), где оба целые ?function search_start_value($price, $sale) {
return $price * 100 / (100 - $sale);
}
echo search_statr_value(1499, 30); // 2141,4285714286
2/3 * sqrt(x^3)
[0, 2346] оказалось 105 из диапазона "B"[0, 1902], т.к. длина "B" 544-101+1 = 444, 2346 - 444 = 1902[0,1902] оказалось, например, 404. Для чисел выше 100 добавляем 444 и получаем 848 из диапазона "C" по старому стилю )
y = x^2 Там на шаге x от 0 до 1, y растет от 0 до 1, на шаге от 3 до 4 y растёт уже от 9 до 16, на 7. Взяв равномерно-случайную величину от 0 до 16, квадратный корень из неё неравномерно попадёт на диапазон от 0 до 4. Вероятнее на диапазон 3-4, чем на 0-1. И вероятность попадания в точку x будет прямо пропорциональна x.
0 000 -> 000 0
1 001 -> 100 4
2 010 -> 010 2
3 011 -> 110 6
4 100 -> 001 1
5 101 -> 101 5
6 110 -> 011 3
7 111 -> 111 7Math.ceil( 18 / 5 ) === 3; // строка с индексом 3, считая от 0
18 % 5 === 3; // колонка с индексом 3, считая, опять же, от 0В языках программирования импликация используется, как правило, неявно. Например, конструкция, предполагающая истинность условия B в данном участке программы:if ( выражение A ) { if ( выражение B ) { сделать_что-то_полезное } else { <font color=Red>сбой</font> }; }
будет успешно выполняться тогда и только тогда, когда верна импликация A→B. В то же время эти условия можно спокойно написать в одной строке, объединив их оператором конъюнкции.if ( выражение A ) and ( выражение B ) { сделать_что-то_полезное }
При стандартных опциях компилятора (Delphi, C++ Builder) проверка идет до тех пор, пока результат не станет очевидным, и если А ложно, то (А и В) ложно вне зависимости от В, и не нужно ставить еще один условный оператор.//выражение A - ложно if ( выражение A ) { //Дальше проверка не идет ... if ( выражение B ) { сделать_что-то_полезное } ... }
В функциональных языках импликация может быть не только правилом вычислений, но и видом отношения между данными, то есть обрабатываться (в том числе и выполняться) и создаваться по ходу выполнения программы.
(x, y, z).(0, 0) и смотрит точно на (0, 0, 0) трехмерного мирка. У экрана ось X вправо, ось Y вверх. В мирке ось x влево, ось y вверх, ось z вдаль.x точно так же добавит X'у экранному. Y чуть меньше из-за угла в 45°. Т.е. y домножим на корень-из-2 пополам.z.X = x;
Y = (y + z) * 0.7071;0 1
1 0