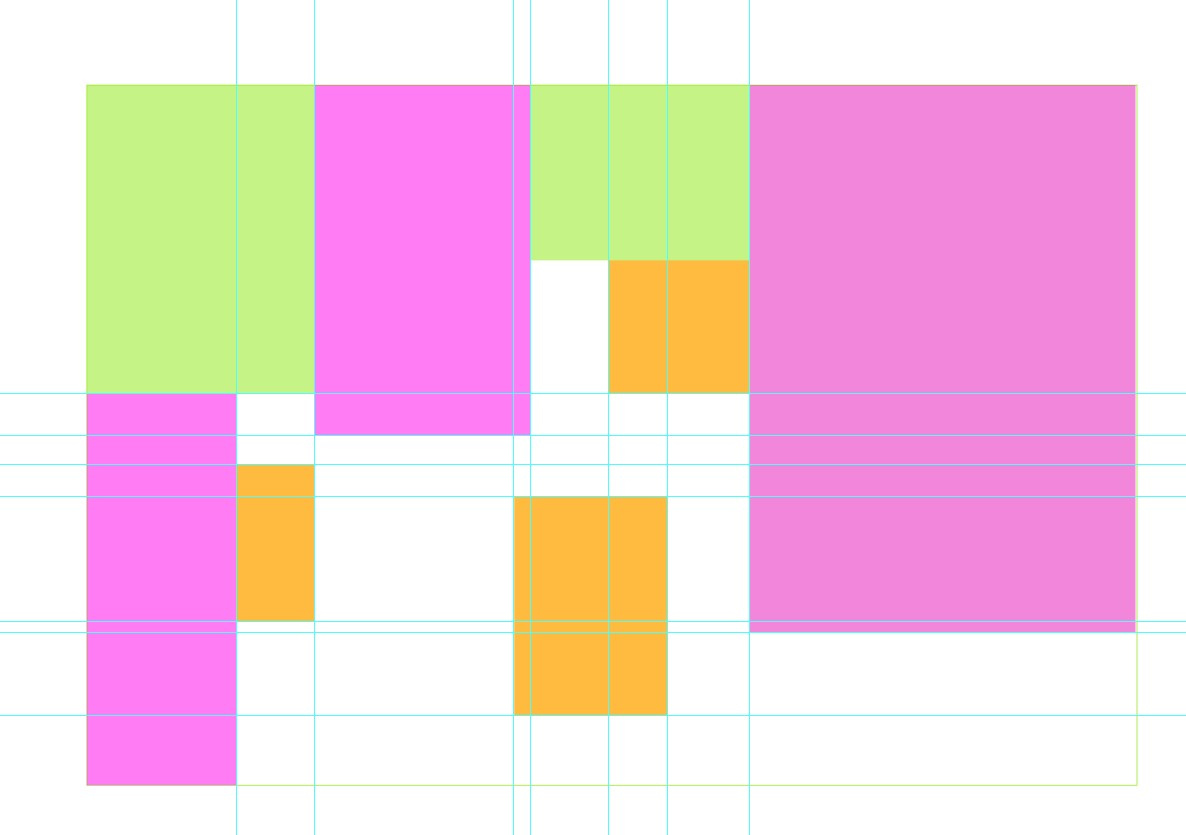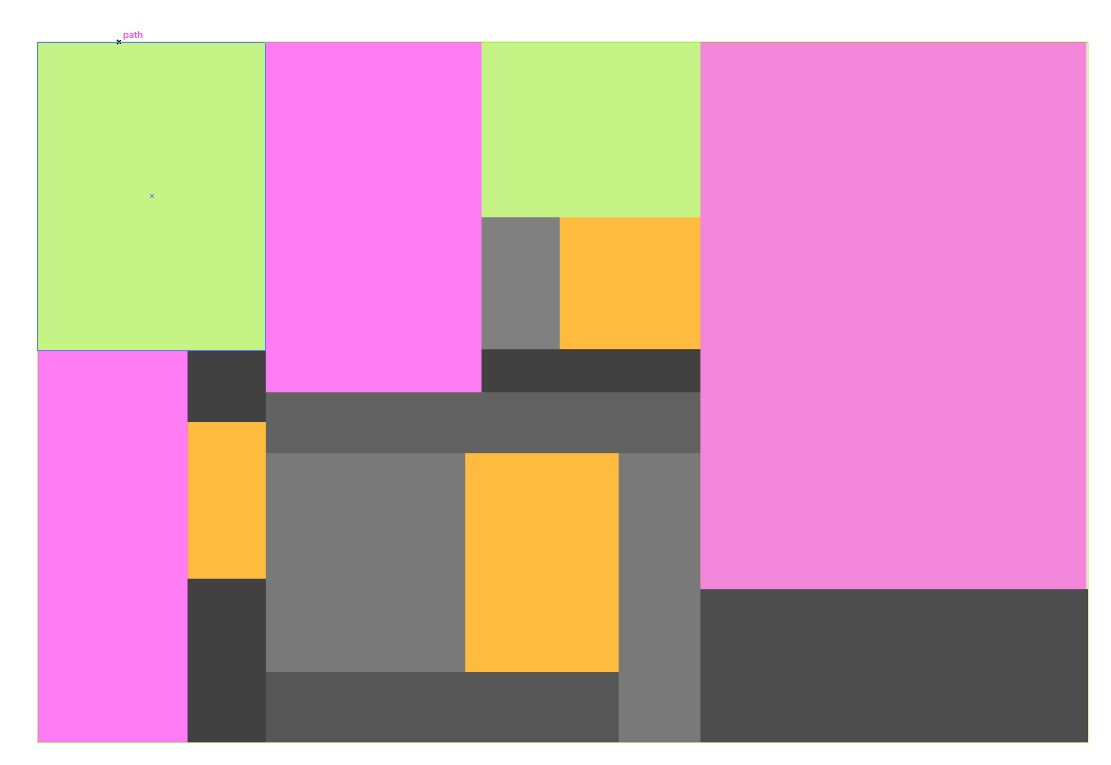Алгоритм поиска пустых прямоугольников?

Question

[Дмитрий Калинин]

Есть поле с заполненным квадратами и пустым пространством. Необходимо из пустого пространства сформировать видимые прямоугольники.
1. Поле:

2. Если начертить направляющие по крайним сторонам видимых квадратов то формируется сетка:

3. Необходимо сформировать наименьшее кол-во цельных прямоугольников из пустого пространства:

4. Для примера изображение выше может быть разбито и так:

или так

А может быть и вообще разбито на множество мелких прямоугольников на пересечении направляющих, но задача сформировать как можно бОльшие прямоугольники и как следствие наименьшее их количество.
Какой алгоритм для такой задачи наилучшим образом подошел бы (оптимальный по быстродействию)?

Answer 1

[Сергей Соколов]

Вроде бы, всё просто. Никакой NP-полноты.

1. Разбить, как вы и описали, по гайдам на мелкие. Это максимальное число полигонов.
   
2. Взять любой, и начать присоединять к нему смежные, насколько возможно.
   
3. Взять следующий пустой не затронутый.
   
4. Процесс останавливается, когда больше ни к одному 4-угольнику нельзя присоединить еще один.
   

Поверхностно кажется, что так получится наименьшее возможное число. Хотя не гарантируется максимизация площадей. Хотя, пожалуй, такой подход может не найти оптимальный вариант, когда границы нескольких исходных блоков легли точно на одной линии. Тогда выиграет вариант, захватывающий обе пустоты. Представьте силуэт буквы «Т». Его можно замостить всего двумя прямоугольниками. Но алгоритм может прозевать такую возможность и предложить 3 блока.

Представьте себе Г-образный набор блоков. Как ни крути, там не менее 2 в итоге получится. Заметьте, что в обоих вариантах у вас получилось по 9 прямоугольников.

П.2 подробнее. Тут возможны разные стратегии. В частности:

• Можно от блока «пойти» в одну сторону, присоединяя соседей, пока не упрётся в непустую область. Затем попытаться расшириться во вторую сторону всеим набранными блоками, до упора. Затем в третью и четвертую.
  
• Можно идти спиралью. 1 шаг наверх, 1 шаг вправо, 1 шаг вниз, 1 шаг влево и т.д. пока подряд 4 шага ни один не даст прироста.
  

Comments

[Дмитрий Калинин]

это более близко думал об этом. логика была такая: вначале создаем матрицу всех пустых точек.[x1...xn] и соответствующие им [y1...yn], потом отсортировать по уменьшению к примеру по x, берем наименьшше x из пустых с наименьшим y, т.е. самую высокую, от нее пускаем вправо луч до столкновения, а потом проверяем на эту ширину максимально возможные пустые координаты с шагом в 1 строку -> пока у нас на ширину заполняются нижние координаты по y то значит там можно построить прямоугольник, как только упираемся, то значит стоп, фиксируем прямоугольник и удаляем координаты из пустых и т.д. А потом составить алгоритм по объединению, что уже проще. Хотя такой метод не дает никаких гарантий что это будут прямоугольники оптимальной площади, но в принципе тоже рабочий вариант. Единственное сомнения на счет подхода: перебирать каждую точку для формирования массива пустых точек или можно оптимизировать?

[Сергей Соколов]

Дмитрий Калинин, координаты целочисленные?
В каком виде даны исходные условия заполненных зон?

[Дмитрий Калинин]

в этом и суть задачи) привести к целочисленным. не буду вдаваться в детали, но блоки которые не соседствуют (у которых нет связи по цепочки с началом координат (верх, лево) ) не имеют целочисленных координат, суть все процесса это округление прямоугольников, их трансформация и последующие смещения для получения сегментов с целочисленными координатами при любом масштабировании всей системы.
вообщем если кратко то нет) вернее не все координаты целочисленные.
но я вижу решение это проблемы путем проверки координаты на границе. если предыдущий x попадал в видимый прямоугольник а следующий в свободную область, то если прямоугольник слева то, то x1.пустоты = x2.видимого, а если пустота справа то то x2.пустоты = x1.видимого. когда границы нет то идет перебор с шагом 1.
только наверное при таком подходе от полного перебора каждой точки не уйти(

[Дмитрий Калинин]

в виде x1, y1, w, h (x2, y2 тоже есть для удобства )

[Дмитрий Калинин]

вообщем основной вопрос построения первоначальных прямоугольников. с объединением более менее понятно, а вот какой метод для сканирования выбрать пока думаю. либо взять за базу какую то ось, например х, отсортировать все х1, х2 по возрастанию и потом с каждой точки пробовать идти в стороны, как я и описывал выше..

[Stalker_RED]

Сергей Соколов,

2. Взять любой, и начать присоединять к нему смежные, насколько возможно.
3. Взять следующий пустой не затронутый.

Обходя сверху слева получите первый вариант.

И это очень простой пример, на практике все может быть намного хуже.

[Дмитрий Калинин]

смотрите, первая задача - определение пустых прямоугольников! как их правильно и быстро (желательно) определить? вот те мелкие, получающиеся на пересечении направляющих. визуально вроде бы просто, а вот с алгоритмом пока заминка.

[Stalker_RED]

Дмитрий Калинин,
1. найти все границы
2. найти углы
3. построить сетку
      3а. перебрать все углы построив сетку горизонтальных линий от угла до ближайшей границы
      3б. перебрать углы еще раз, построив вертикальные, и пересечения

[Сергей Соколов]

Stalker_RED, первые два примера дали оба по 3 прямоуголника. Во втором есть два совсем мелких, но на общее их число это не повлияло. ПРо второй кейс с Т-образной формой я уже писал: да, это потенциальная проблема. Которая, впрочем, решается перебором 4-х вариантов направления начала. Худший кейс тут 4 центрально-симметричных буквы Т, направленные как стрелки часов в 4 разные стороны.

К счастью, в условиях конкретно этой практической задачи, возможно, исключается попадание двух заполненных граней точно на один гайд с разрывом.

[Stalker_RED]

Сергей Соколов,

но на общее их число это не повлияло

но задача сформировать как можно бОльшие прямоугольники

[Сергей Соколов]

Stalker_RED, оригинальная цитата:

задача сформировать как можно бОльшие прямоугольники и как следствие наименьшее их количество

из этого я предположил, что, возможно, конечная цель именно минимум фигур, а не наибольшая их площадь.

Да и от перестановки мест слагаемых сумма не меняется )
4 + 4 + 20 = 1 + 2 + 25

[Stalker_RED]

Сергей Соколов, общая площадь не изменится даже если все однопиксельными блоками замостить.

Answer 2

[Stalker_RED]

https://en.wikipedia.org/wiki/Covering_problems
В частности: https://en.wikipedia.org/wiki/Polygon_covering#Cov...

Comments

[Дмитрий Калинин]

ну а где там собственно сам ответ?)

[Stalker_RED]

Дмитрий Калинин, это NP-полная задача, но для простых фигур есть приблизительные решения за примерно полиномиальное время. И ссылки на литературу, где решения описаны.

(никто не говорил, что задача простая)

Говоря попроще: наилучшее решение вы получите только перебрав ВСЕ варианты, а это долго, если фигура сложная. Но если нужно не самое-самое, то можно решить и побыстрее, и какие-то чуваки из университетов уже придумали как, и написали про это книжку, или диссертацию, или типа того. И ссылки на публикацию есть.

Answer 3

[profesor08]

Бегаешь по прямоугольникам, если грани формирующие угол соприкасаются с пустотой, то тяни одну из граней до упора. Так получишь еще один прямоугольник. Его надо запомнить. Аналогично проделать со всеми углами. Далее объединяешь два соседних получившихся прямоугольника в один, если их соприкасающиеся грани одинаковые. Так ты получишь наименьшее количество прямоугольников из пустой области. Конечный результат зависит от того, в какой последовательности ты все будешь делать, главное не плоди слишком много мелочи, и старайся из одного угла тянуть только одну грань.

Answer 4

[Дмитрий Калинин]

вообщем тут думаю такой ход действий. тест грани на сосесдство с пустотой--->в зависимости от стороны которая соседствует формируем массив видимых блокоы лежащих на ее пути и сортируем по наименьшей координате (в зав-ти от стороны, если правая сторона базового блока то сортируем то что справа по х1, слева по х2 и т.д.) ---> формируем блок и перезапускаем заново цикл, каждый новый найденный блок помечаем ---> когда пустота закончится прогоняем циклом все помеченные найденные блоки на возможность слития. как то так наверное

Comments

[Сергей Соколов]

если вдруг тесты алгоритма будете делать на JS, поделитесь песочницей, интересно.

Answer 5

[majalineage]

все очень просто. с начало добавляем рект на все поле в некий лист nodes. потом бежим по всем ректам которые есть на поле, пусть он будет CurrentRect, и для каждого выполняем алгоритм:
бежим по всем nodes от i = 0 до nodes.Count - 1 (во время пробегания nodes.Count может меняться)
{
Берем nodes[i] и если он пересекается с CurrentRect (именно пересекается а не касается) выполняем следующее:
{
Обрезаем его по CurrentRect. как именно: с начало снизу, если есть что резать пихаем в nodes новый рект а текущий урезаем по CurrentRect, и так по всем сторонам
Первый в прогоне запоминаем как основной, который в итоге останется на месте CurrentRect, если он меньше CurrentRect, растягиваем его по CurrentRect.
Все остальные после разрезаний удаляем (куски которые будут лежать в CurrentRect, они лишние) и делаем i--
}
}
Далее можно сделать оптимизацию, найти ректы с одинаковыми гранями и объединить их. Еще можно что-то придумать. Но это уже задачка по легче