RPG = Dragon_Age, The_Elder_Scrolls_Skyrim Плохая структура, которая потребует парсинга, сами себе создаем проблемы. import json
data = {
"RPG": ["Dragon_Age", "The_Elder_Scrolls_Skyrim"],
"Action": ["Grand_Theft_Auto_V", "Watch_Dogs"],
"MMORPG": ["Lineage_2", "Aion"],
"Shooter": ["Bulletstorm", "Splinter_Cell"],
"Racing":["Need_For_Speed_Payback", "Blur"]
}
with open("data.json", "w") as f:
json.dump(data, f)with open('data.json', 'r') as f:
json_object = json.load(f)shuffle (перемешать элементы) и выбирать элемент c нулевым индексом всегда.from random import shuffle
genres = list(json_object.keys())
shuffle(genres)
genre = genres[0]
print(f'Вам выпал жанр: {genre}')
games = json_object[genre]
shuffle(games)
game = games[0]
print(f'Вам выпала игра: {game}')pop у списка и получим эффект выборки без замены (Но надо понимать объект json_object будет изменяться). Можно пойти и вашим путем. Осуществлять выборку индекса и выбирать по индексу, тоже нормальное решение.import os
os.system("conda env list")import yfinance as yf
btc_usd = yf.download('BTC-USD')import numpy as np
arr1 = np.ones(9).reshape(3,3)
arr2 = np.ones(8).reshape(2,4)
arr1 + arr2import numpy as np
arr1 = np.ones(27).reshape(3,3,3)
arr2 = np.ones(9).reshape(3,3)
arr1 + arr2
pd.read_json() во вторых есть метод json_normalize() если json содержит "вложенные словари". Приведи в порядок свой датафрейм, и данные запишутся в базу. Не знаешь, как привести датафрейм в порядок, показывай его и отдельным вопросом. import pandas as pd
import numpy as np
data = [
{'symbol': 'FTTBUSD', 'positionAmt': '0.001', 'entryPrice': '0.0', 'markPrice': '0.00000000'},
{'symbol': 'ETHUSDT', 'positionAmt': '0.003', 'entryPrice': '1912.07', 'markPrice': '1911.37031373'},
{'symbol': 'ALPHAUSDT', 'positionAmt': '0.002', 'entryPrice': '0.0', 'markPrice': '0.00000000'}
]
df = pd.DataFrame(data=data, columns=['symbol','positionAmt'])
df['positionAmt'] = df['positionAmt'].astype(float)
print(df)df.plot(kind='bar', x='symbol', y='positionAmt'); Выведет вот такой график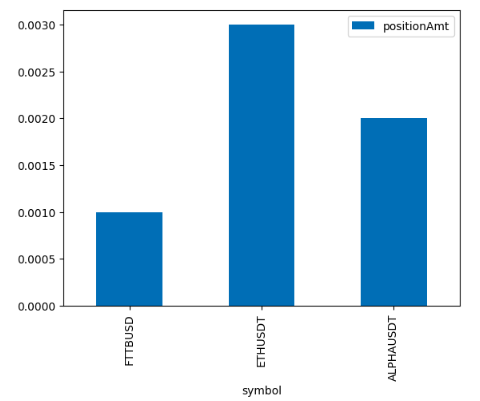
print(klicker.__dict__) и там увидишь вот такую строчку '_lines': {'event': matplotlib.lines.Line2D at 0x7fe0e34a1a50}, далее если глянуть документацию класса Line2D то мы увидим что 'linestyle' это property. klicker._lines['event']._linestyle Это даст тебе стиль линии. Изменить его можно (но это property) защищенный атрибут то есть можно но не нужно, так или иначе.klicker._lines['event']._linestyle = '-' его изменит. data = [('Ivanov','Ivan',None), ('Petrov','Petr',30),...,('Sidorov',None,None)]
columns = ['name','surname',...'age']
df = pd.DataFrame(data, columns = columns)
df.to_csv('result.csv',header=False, mode='a')cls(*args, **kwargs) Вызывается просто MyClass.classmeth(*args, **kwargs) DataFrame(data) А можешь использовать методы класса для альтернативного метода создания экземпляра (из другой структруры) DataFrame.from_dict(some_dict) так вот from_dict это метод класса. class MyClass:
currency = 'Dollar'
def __init__(self, amaunt):
self.amaunt = amaunt
def __str__(self):
return f'MyClass({self.amaunt, self.currency})'
@classmethod
def euro(cls, amount):
cls.currency = 'Euro'
return cls(amount)
dollar = MyClass(100)
print(dollar)
euro = MyClass.euro(100)
print(euro)Говорю сразу, я в программировании в целом почти что новичок, и опыт с питоном имею чуть больший, чем сдающие с ним ЕГЭВаша задача для опытных программистов с релевантным опытом.