Как считать очень большие числа, и на каком языке программирования?

Question

[Игорь Васильев]

Здравствуйте.
--
Очень прошу отнестись к этому вопросу со всей серьёзностью. Хочу знать именно экспертное мнение программистов и математиков. Так вот, суть вопроса. В мире есть очень огромные числа, и их наверняка как-то считают, чтобы вы понимали, в этих числах астрономически огромное число нулей, не один современный калькулятор не способен ввести себя хотя бы одно число, не говоря уже о том, чтобы умножить, прибавить, разделить, вычесть или возвести в степень второе число. Чтобы не тратить целый день на то, чтобы написать только одно число для примера, я прилагаю

весь список чисел который удалось найти

Единица
Десять
Сто
Тысяча
Миллион
Миллиард
Триллион
Квадриллион
Квинтиллион
Сикстиллион
Септиллион
Октиллион
Нониллион
Дециллион
Вигинтиллион
Центиллион
Миллеиллион
Мириада
Гугол
Асанкхейя
Гуголплекс
Второе число Скьюза
Мега
Мегистон
Мозер
Число Грэма
Стасплекс
Авогадро.

не знаю, может ли быть что-то ещё больше чем последнее число в этом списке. Так вот, что-то мне подсказывает, что обычной вычислительной мощности компьютера может не хватить при вычислении таких чисел. Соответственно нужен и соответствующий язык программирования, который будет в состоянии считать хотя бы числа Грэма, не говоря уже о грэмаплексе.

Чтобы вы понимали, я говорю не о маленьких числах по типу:
263.130.854.592.673.365.047.218.012.160.000.000.000.000.000.000

А о числах в которых может быть и миллион и квинтиллион цифр. Я ещё не пробовал посчитать такие числа на Python - но очень интересно, получится ли такое посчитать. В php я рискнул только с цифрами не превышающими 50 знаков. И код считает эту простую операцию очень долго. И зачастую вставляет букву "е" в число. Никаких букв при вычислении быть не должно. Если введу число в котором миллион цифр, боюсь этим сжечь ЦП ))
Может даже памяти не хватит.
Поясню, что простые операции с числами - это тест, если я найду способ считать огромные числа, это потом понадобится для вычисления матриц, степеней, триангуляционных решений и получения корней.
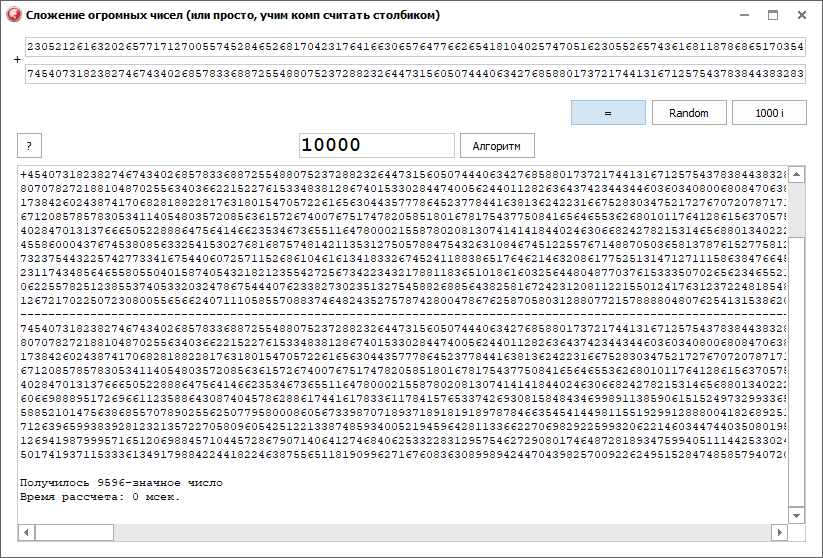
Чтобы оценить сложность этой задачи, покажу не очень большие цифры, которые помещаются на экране.

Вы могли их уже видеть, ну вдруг кто не имеет представления.
Конечная цель, это измерение площадей, расстояний и 3х мерных неровных пространств.

Благодарю всех кто с пониманием и с серьёзностью отнёсся к этому вопросу. Надеюсь среди нас есть кто-то, кто представляет как это всё считать.
Возможно это будет знакомо понятно и интересно тем, кто изучает астрономию.
https://spacegid.com/interaktivnaya-shkala-masshta...

Comments

[vreitech]

> который будет в состоянии считать хотя бы числа Грэма
за Грэма и всё что рядом можете даже не пытаться браться, с точностью до каждой цифры вы их не посчитаете.

> Может даже памяти не хватит
вам не хватит всего: памяти, производительности и времени.

[Алан Гибизов]

vreitech, совершенно согласен.
А ещё добавлю, что считать гигантские объёмы и площади в пространстве несколько малополезно, с учетом того, что само пространство прирастает со скоростью 72 км/с на каждый мегапарсек. То-есть, пока Вы считали, пространство приросло и вычисленный объём устарел :)

[Алан Гибизов]

И потом: практически никто не делает непосредственных вычислений с гигантскими значениями. Зачем? Вычисления делают с абстрактными значениями, обозначенными буковками alpha, beta, gamma ... omega, и смотрят на их итоговое соотношение. И оценивают, что если вот тут будет дохрениллиард, то он вот тут поделится на афигиллион в степени непредставиллиард и в итоге будет число стремиться к нулю. И зачем сами вычисления-то проводить?

Answer 1

[Владимир Коротенко]

Не такие и большие числа :)
https://github.com/aleaxit/gmpy

Кроме того посмотрите в сторону Fortran, там много готовых библиотек именно для научных вычислений.

В общем случае библиотеки есть для любого ЯП

Comments

[Денис Загаевский]

Это не научные вычисления, это профанация.

[Игорь Васильев]

Напоминает чем-то питон. Благодарю, заинтересовало.

Answer 2

[6yntar05]

Не претендую на решение, но думаю что число лучше записывать в String или похожую строку и частями считать

Comments

[Иван Карманов]

Полностью согласен, можно ещё записать в одну переменную значимые цифры, а в другую степень 10, т.е. количество нулей, а после операций с значимыми числами просто нули дописать

[Игорь Васильев]

Интересное решение. Вы я так понимаю, так считали? Есть погрешности?

[6yntar05]

Игорь Васильев, я так никогда не делал. Но это вполне реализуемо. Погрешности такие-же как и при обычном счёте(да нет их крч)

[Hemul GM]

6yntar05, я как раз так делал. Ниже ответ написал.

Answer 3

[mayton2019]

Любая библиотека с поддержкой arbitrary-precission подойдёт.

Но мне кажется что автору это не надо. Физические величины (расстояния) невозможно менять настолько точно чтобы уже 40 младших знаков имели смысл.

Comments

[Игорь Васильев]

Я попробую эту библиотеку. И скажу вам точно. В любом случае благодарю за информацию

Answer 4

[Griboks]

Если кратко, то это невозможно.

Если подробно, то используют всякие уловки:
1. символьные вычисления (когда мы упрощаем формулы вместо чисел)
2. относительная точность (когда мы обнуляем ненужные знаки)
Так, число Авогдаро = R/k = 6е23, и нет там никакого огромного количества цифр.

Но если вы хотите убедиться в невозможности решения, тогда просто перейдите от двоичной/десятичной системы счисления в, например, байтову. Тогда ваше число можно записать как BigInt:

sign*(type_size^n*array[n]+...+type_size^1*array[1]+type_size^0*array[0])

Заметим, что длина массива тоже имеет определённый тип, поэтому вам придётся использовать списки. Останется только реализовать нужные вам операции. Посмотрите реализацию BigInt в вашем языке.

Comments

[Рональд Макдональд]

Если кратко, то это невозможно.

Лол.
Откройте для себя Matlab и Maple.

[Денис Загаевский]

Рональд Макдональд, открой для себя число Грэма и прибавь к нему единицу. Потом вместе посмеемся.

[Griboks]

Рональд Макдональд, видимо, открыл не стой стороны. А может мне попался просроченный, но не смог найти ничего подобного. Не могли бы привести примеры?

[Игорь Васильев]

Если кратко, то это невозможно.

Для человека нет ничего невозможного. Когда-то был бум на криптовалюту, и все с пеною у рта кричали, что нельзя создать и спрограммировать такой валидатор, который бы проверял фиктивны криптокошелёк или реальный. Нигде в интернете не было решения. Думаете меня это остановило? Я написал такой валидатор.

2. относительная точность (когда мы обнуляем ненужные знаки)

Нет страшнее человека, который игнорирует точность в математике. Из-за таких вот людей и разбиваются самолёты, ракеты и шаттлы. Малейшая погрешность в расчётах может стоить жизни многим людям. Математика - это точная наука. И она мстит людям за все приблизительные и на глаз вычисленные решения. Для вас последние цифры могут быть ненужными и незначительными знаками, а в реальности из-за этого может разбиться о поверхность планеты чей-то космический модуль на несколько миллионов долларов. Вы опасный человек...

[Денис Загаевский]

Игорь Васильев, что ты такое несёшь...

[Griboks]

Игорь Васильев,

Для человека нет ничего невозможного.

Ну, если вы докажете, что, несмотря на невозможность записать число грэма в объёме видимой вселенной, компьютер не только умеет хранить несколько таких чисел, но и владеет арифметикой над ними... то будет уже хорошо. Затем останется только построить такой компьютер.

На текущий момент таких гениев ещё не было, поэтому люди используют аппроксимацию.

Нет страшнее человека, который игнорирует точность в математике. Из-за таких вот людей и разбиваются самолёты, ракеты и шаттлы.

Так всё же в математике или ракетостроении? Какой по-вашему мнению гравитационный коэффициент должны использовать конструкторы, если он постоянно меняется, его нельзя точно измерить, является бесконечной дробью?

Малейшая погрешность в расчётах может стоить жизни многим людям.

А вы из тех людей, которые округляют числа до 100500 знаков после запятой, чтобы ответ получился точнее?)) По этой теме можете почитать ГОСТ по округлению.
Ну и так далее...

Мне кажется, что вы ещё студент или школьник, который не осознаёт, что такое точность , округление и погрешность.

[Игорь Васильев]

Griboks, не то и не другое. Просто общение с умными людьми раскрыло мне сознание, что такое математика (я понял в чём смысл). И эта наука меня заинтересовала, хотя ранее я её не понимал и не воспринимал. Что касается компьютеров, есть у меня одна теория, которую я хотел исследовать в лабораторных условиях, осталось подсчитать сколько этот эксперимент будет стоить и где лучше всего его проводить.

[Игорь Васильев]

Денис Загаевский, я несу свет людям ))

[Денис Загаевский]

Игорь Васильев, ты и теперь её не понимаешь. Просветлённый, блин. Либо тролль, либо идиот.

Answer 5

[Рональд Макдональд]

Используйте метематические пакеты типа Mapleили Matlab.
Есть бесплатные аналоги.

Answer 6

[Hemul GM]

Я как-то давно делал подобное приложение. Хотя, делал только сложение чисел. Пришлось делать 64bit версию, чтобы считать числа "длинной" в больше чем миллионы знаков. Делал на Delphi. Код достаточно скромный.
https://github.com/HemulGM/HandleSumm

Comments

[Hemul GM]

Ну и вот пример ещё. В полях сверху числа не отображаются, т.к. компонент сходит с ума.

[Hemul GM]

Алгоритм можно настроить на работу с потоком, т.е. использовать не ОЗУ, а дисковую память, но конечно, производительность упадёт.

[6yntar05]

Страшно, вырубай

[Hemul GM]

6yntar05, у меня где-то было фото (не скрин), где я тестировал это приложение и оно, из моих тогда 6гб озу съело 16гб. Комп встал намертво и висел минут 15. Но посчитал.

Answer 7

[Yermack]

Таки попробуйте питон: единственное что ограничивает это оперативка. Почти полмиллиона знаков весом почти четыре сотни Мб посчитало за 3сек

import sys

X = 124456**78901

sys.getsizeof(str(X))/1024, len(str(X))
# (392.6279296875, 402002)

Хотя на Джулии получилось быстрее

julia> @time X = BigInt(124456)^7890123;
  0.848368 seconds (6.49 k allocations: 146.362 MiB, 9.79% gc time)

julia> length(string(X))
40200302

Answer 8

[Лёшик]

Даже если вы возьмёте первый из Top-500 суперкомпьютеров и, отбросив всё устройство компьютера, сможете использовать всю его оперативную память (250 петабайт) для кодирования одного единственного числа, то максимальное будет иметь (очень грубая оценка) всего 6.7*10^17 знаков. Даже близко не гуголплекс :)

Comments

[Игорь Васильев]

XD XD XD - прям инструкция как запустить ЦП и память компьютера в космос.
Дико угорел, ухаха!
Калькулятор:
- К таким подсчётам, разработчики меня не готовили )))

[h8nor]

Игорь Васильев, для запуска чего-либо в космос не нужны числа большого порядка.

Answer 9

[evgeniy_lm]

Понятие "точность расчетов" хорошо иллюстрирует анекдот:
Экскурсовод в музее:
- Этому экспонату примерно 3005 лет.
Экскурсант:
- Как вы так точно определили!?
Экскурсовод:
- 5 лет назад, когда я устраивался на работу, директор сказал, что этому экспонату примерно 3000 лет

В реале большие точные числа нужны только в алгоритмах шифрования и ни где более.
Как правило большое число представляется в виде массива байт и есть соответствующие функции их обработки. Я, даже, давно сам этим баловался, ничего сложного там нет.
Ваш ГУГОЛ это всего навсего 42 байта, а алгоритмы RSA используют числа длинной 64 и более байт
Еще есть алгоритмы вычисления числа пи, но это немного другая история которая практической пользы не имеет

Comments

[h8nor]

Пользы может и не имеет, а вот применение есть factordb.com/index.php?query=2%5E1277-1

[evgeniy_lm]

Дѣаволъ, Применение к чему?

[h8nor]

evgeniy_lm, применение для поиска делителей больше 2⁶⁴

[evgeniy_lm]

Дѣаволъ, Может не делителей, а наоборот простых чисел? Ну, дык, это вопросы алгоритмов шифрования (я об этом написал). Другой надобности в столь огромных числах просто не существует

[h8nor]

evgeniy_lm, если нет других делителей кроме самого простого числа, то да (но в примере число не является простым по тесту Люка-Лемера, хотя сегодня не найдено ни одного делителя).
Хм, вот и нашлось практическое применение - стресс-тест железа ;)