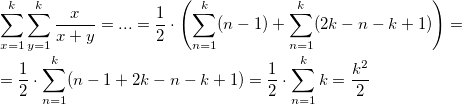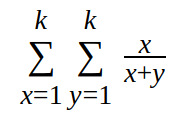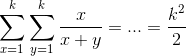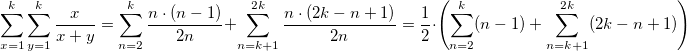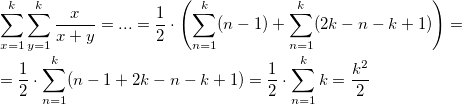Как оптимизировать сумму ряда?

Question

[Александр]

Доброго времени суток, подскажите как можно оптимизировать алгоритм по подсчету ряда для больших значений k?

Answer 1

[Rsa97]

Аналитически.

Я нашёл этому поистине чудесное доказательство, но поле ввода слишком узко для него. (C) Ферма.

Решение

Рассмотрим дроби - слагаемые данной суммы. Очевидно, что знаменатели могут меняться от 2 до 2k.
Попробуем определить, какие числители будут в дробях со знаменателем n. Для этого нам надо разложить n на пары x и y всеми возможными способами, учитывая ограничения 1 ≤ x ≤ k, 1 ≤ y ≤ k и взять допустимые значения x.
Если 2 ≤ n ≤ k, то допустимыми значениями x будут 1 ... n-1. Для k+1 ≤ n ≤ 2k допустимыми значениями x будут n-k ... k. Таким образом, мы можем записать сумму числителей для каждого знаменателя:

Теперь, с учётом полученной системы запишем, как будет выглядеть полная сумма всех дробей:

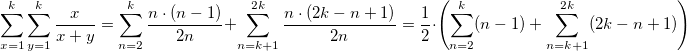
Заметим, что если в первой сумме начать суммирование не с 2, а с 1, то сумма не изменится, поскольку добавленное слагаемое равняется нулю. Во второй сумме перенесём k из пределов суммирования в слагаемое. Получим две суммы с одинаковыми пределами, а значит их можно объединить в одну:

Comments

[d'Ivan]

limit?

[Сергей Соколов]

Роман Мирр, нет, т.к. верно и на малых k