Есть ли алгортм покрытия окружностями всей площади произвольной фигуры?

Question

[WTFRU7]

Вопрос чисто математический, но приведу пример из жизни, так сказать.

Итак, задача в следующем - есть произвольная фигура на карте (может быть как выпуклая, так и вогнутая).
Представим, что мы - сотовый оператор, который хочет покрыть базовыми станциами город. У каждой станции радиус действия фиксированый и зона покрытия имеет форму окружности. Нужно найти оптимальный способ, как наименьшим количеством базовых станций покрыть всю внутреннюю территорию фигуры. Избыточность допустима.

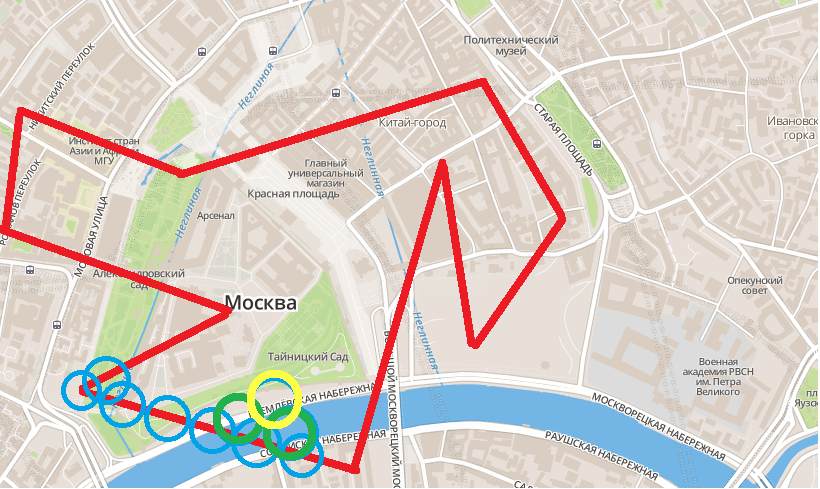
Моя идея такова - строим окружность на любом угле фигуры, так, чтобы ее центр был ровно на точке пересечения 2 граней фигуры. Далее строим такую же окружность на точке пересечения грани фигуры и первой окружности - и так пробегаем по всему периметру фигуры (голубые окружности). Далее строим окружность с центром в точке пересечения 2 голубых окружностей (зеленые). И так пробегамся по всему ряду голубых окружностей. Получается, что на каждой итерации мы будем продвигаться все глубже и грлубже к центру фигуры.
Но, думаю, что мой алгоритм совсем не оптимален.

Главное в задаче - покрыть всю территорию фигуры, при этом использовать минимум станций.

Может быть кто-то сталкивался с подобным? Буду благодарен любым знаниям или гипотезам. Спасибо!

Comments

[extempl]

Чисто касательно примера - насколько мне известно, базовые станции покрывают площадь в виде неперекрывающихся многоугольников, отчего сеть такого рода и была названа сотовой.

Answer 1

[Андрей]

Генетические алгоритмы, мне кажется, будут просто идеальны для этой задачи.

Answer 2

[extempl]

Учитывая, что в вашем варианте решения синие и жёлтые круги будут составлять не что иное, как сетку - можно попробовать наложить на многоугольник сетку с шагом равным диаметру окружности, затем заполнить все целые квадраты (которые целиком лежат в пределах окружности), а затем нарисовать круги на пересечении линий сетки, которое лежит в зоне многоугольника и не было покрыто. После всего этого может остаться ещё непокрытая зона в виде узких полос, на территории которых нет ни центров ячеек сетки, ни точки пересечений линий. Их, видимо, прийдётся обойти по порядку - сначала покрыть целиком ячейки, часть которых лежит на таких линиях, затем, если остались свободные непокрытые места - на пересечениях вокруг этих самых заполненных ячеек.
По сути, изначально, для пущей эффективности, нужно было наложить две сетки - вторую со смещением x+=50%, y+=50% от ширины ячейки. Тогда заполнять только ячейки не обращая внимания на пересечения (они будут центрами ячеек в другой плоскости).

Я думаю, как-то так. Наверняка можно оптимизировать ещё, чтобы в конце (там где линии) не перебирать круги вокруг ячеек вслепую, а рисовать только там, где часть их точно покроет зону.

Ещё, этот алгоритм удобнее и оптимальнее в плане работы с ним, но для покрытия наименьшим кол-вом станций, возможно нужно будет рисовать сетки так, чтоб одно из направлений линий составляющих её было параллельно самой длинной прямой стороне многоугольника. Но не факт, тут надо экспериментировать.