Первый вопрос был какова цель поездки, я ответил что безработный.
friend and Encapsulation
Some people believe that the idea of having friend classes violates the principle of encapsulation because it means that one class can get at the internals of another. One way to think about this, however, is that friend is simply part of a class's overall interface that it shows the world. Just like an elevator repairman has access to a different interface than an elevator rider, some classes or functions require expanded access to the internals of another class. Moreover, using friend allows a class to present a more restrictive interface to the outside world by hiding more details than may be needed by anything but the friends of the class.
Finally, friends are particularly common in cases of operator overloading because it is often necessary for an overloaded operator to have access to the internals of the classes that are arguments to the operator.
Typical use cases of friend functions are operations that are conducted between two different classes accessing private or protected members of both.

Во всех основных разработках используется VisualStudio и тулзы, которые работают только под Windows

В такой (уточненной) постановке задаче интересная и нетривиальная.
Позвольте предложить некоторое огрубление, которое по моему мнению исходя из предметной области не сильно отдалит субоптимальное решение от оптимального, но позволит уйти от геометрии к дискретной математике :
Введем в указанном помещении декартовы координаты так, чтобы препятствия находились строго по границам единичных клеток.
Добавим следующие предположения/ограничения:
а) источники сигнала размещаем только в центрах клеток,
б) считаем, в каждом из четырех диагональных направлений сигнал не виден в клетках, размещенных за углом (углами) любого препятствия (см. рис.)
в) в четырех прямых направлениях сигнал очевидно не виден за первым же препятствием а также нигде далее этой координаты (см.рис.).
Как результат для каждой ячейки как потенциального места расположения сигнала возможно определить булеву матрицу доступности ячеек.
В целом задача сводится к тому, чтобы найти минимальный набор таких выбранных матриц (соответствующих ячейкам расположения источников), который бы обеспечивал полное покрытие помещения.
Мне кажется, что при больших размерах матриц эффективно это реализуемо только алгоритмами эвристического поиска (я сторонник генетических алгоритмов, но конечно есть и другие подходы). 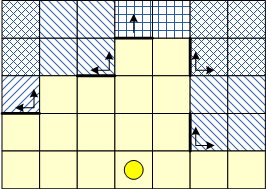
Мне эта многоходовка представляется так:
1. Плоскость с препятствиями делится на прямоугольники (тут тоже стоит подобрать алгоритм)
2. http://ru.wikipedia.org/wiki/Упаковка_шаров
Про производительность JS не скажу, зависит от количества шаров и выбранных алгоритмов.