Нужно расположить источники сигнала (окружности) на прямоугольной плоскости, в которой заданы прямолинейные препятствия. Вопросы:
1) Какие алгоритмы подходят?
2) Какие варианты существуют (более, менее оптимальные алгоритмы, перебор)?
3) Потянет ли такие расчёты JavaScript?
Заранее спасибо за ответы, буду рад ответу даже на один из приведённых пунктов! :)
UPD. Некоторые уточнения, которые сам недавно узнал: конкретная цель - покрыть всё помещение сигналом, при том оптимально и не допустить пересечения источников в ближней зоне; радиус действия каждого источника можно положить бесконечным.

В такой (уточненной) постановке задаче интересная и нетривиальная.
Позвольте предложить некоторое огрубление, которое по моему мнению исходя из предметной области не сильно отдалит субоптимальное решение от оптимального, но позволит уйти от геометрии к дискретной математике :
Введем в указанном помещении декартовы координаты так, чтобы препятствия находились строго по границам единичных клеток.
Добавим следующие предположения/ограничения:
а) источники сигнала размещаем только в центрах клеток,
б) считаем, в каждом из четырех диагональных направлений сигнал не виден в клетках, размещенных за углом (углами) любого препятствия (см. рис.)
в) в четырех прямых направлениях сигнал очевидно не виден за первым же препятствием а также нигде далее этой координаты (см.рис.).
Как результат для каждой ячейки как потенциального места расположения сигнала возможно определить булеву матрицу доступности ячеек.
В целом задача сводится к тому, чтобы найти минимальный набор таких выбранных матриц (соответствующих ячейкам расположения источников), который бы обеспечивал полное покрытие помещения.
Мне кажется, что при больших размерах матриц эффективно это реализуемо только алгоритмами эвристического поиска (я сторонник генетических алгоритмов, но конечно есть и другие подходы). 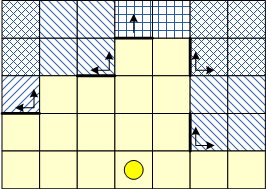
Мне эта многоходовка представляется так:
1. Плоскость с препятствиями делится на прямоугольники (тут тоже стоит подобрать алгоритм)
2. http://ru.wikipedia.org/wiki/Упаковка_шаров
Про производительность JS не скажу, зависит от количества шаров и выбранных алгоритмов.

У любой расстановки есть какая-либо цель. Какая у Вас ?
Покрыть всё пространство сигналом ?
Или наоборот не допустить пересечения сигналов в точке ?
Равны ли диаметры окружностей ?
По какому критерию оптимизируем ?
Задача пока что неясна.