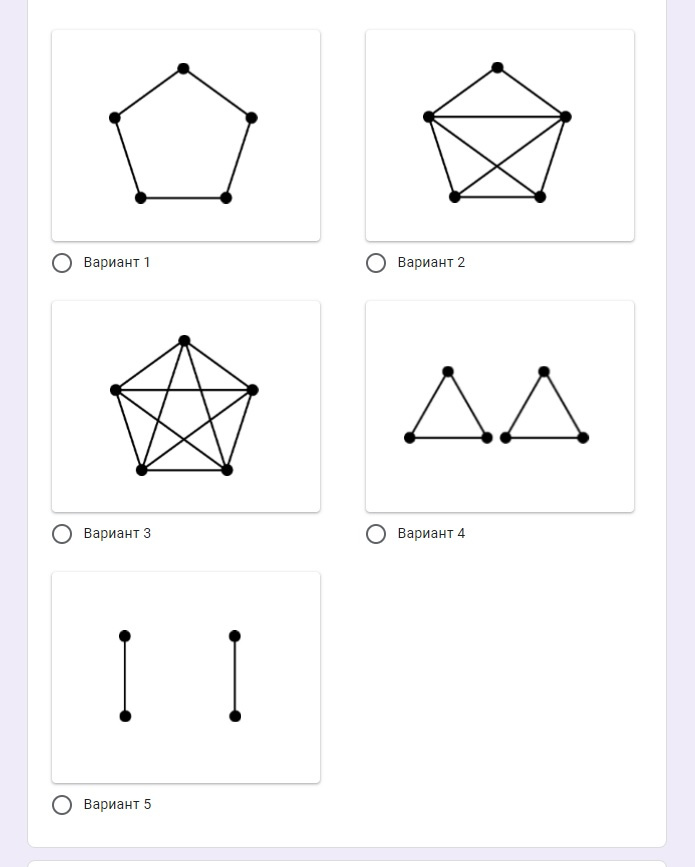
Всем привет, подскажите пожалуйста, как решить следующую задачу?
Существует утверждение "Каждый связный граф имеет одну или несколько вершин степени 2". Ниже представлены 5 графов с 1 или более связанных вершин. Какой из 5 графов является контрпримером описанного утверждения?
Контрпример - это тот, который опровергает утверждение.
Утверждение - каждый связный граф имеет хотя бы одну вершину степени 2.
Т.е. контрпример - связный граф, который не имеет ни одной вершины степени 2.
Степень вершины - это сколько ребер в нее входит. Можете найти такой граф на картинке?
