Потребовалось вписать круг в нестандартную фигуру.
Моё построение было следующим:
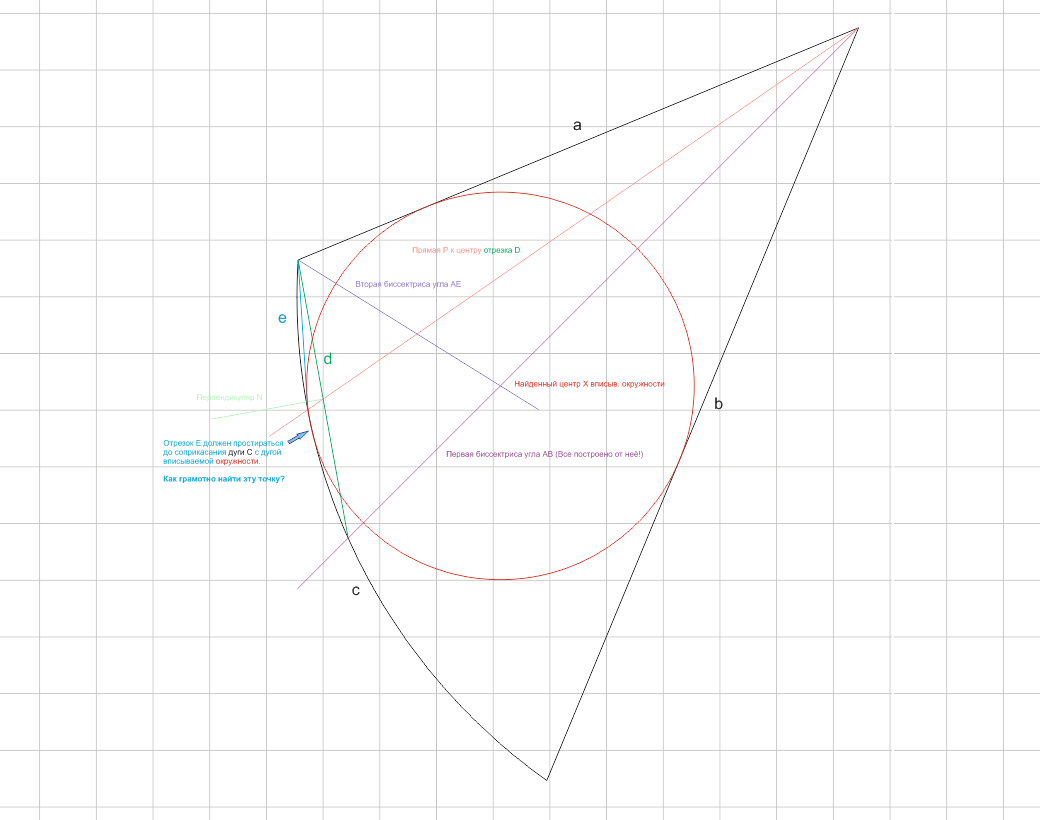
1. Из угла AB провёл первую биссектрису;
2. Из угла AC провёл отрезок D к пересечению биссектрисой AB дуги C;
3. Из угла AB провёл прямую P к центру отрезка D;
4. Из угла AC провёл отрезок E к пересечению прямой P дуги С;
5. Из угла AE провёл вторую биссектрису;
6. На пересечении двух биссектрис найден приблизительный центр вписываемой окружности.
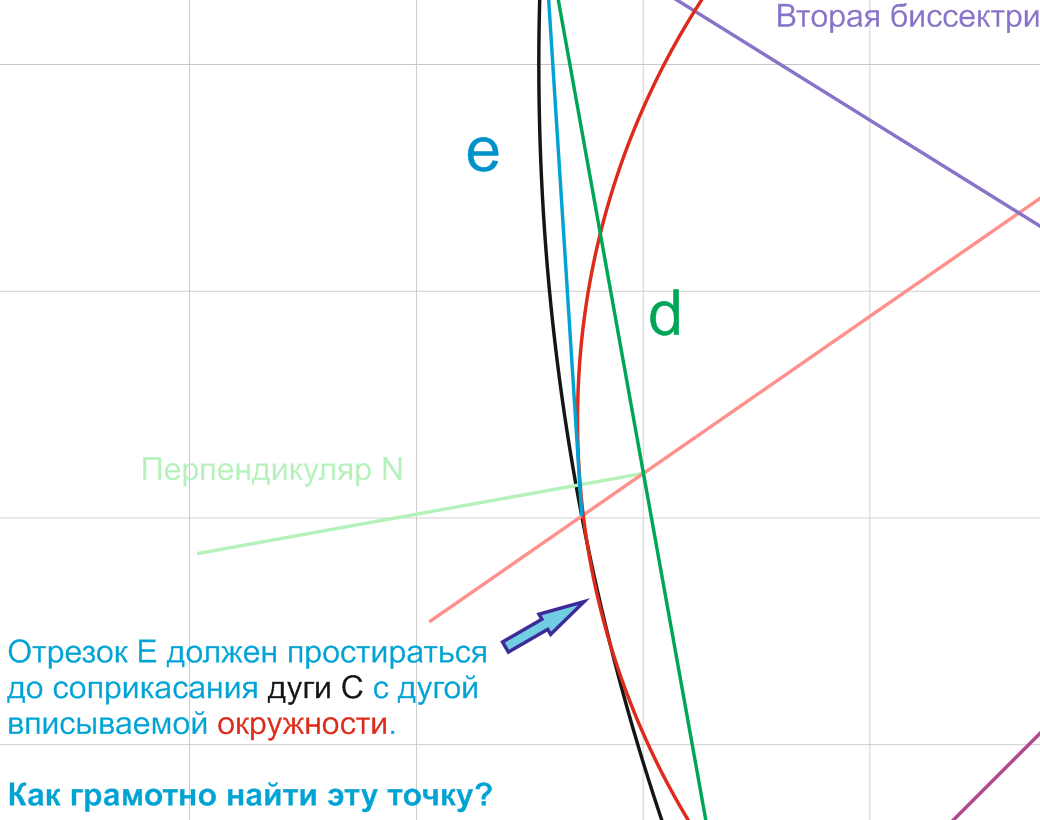
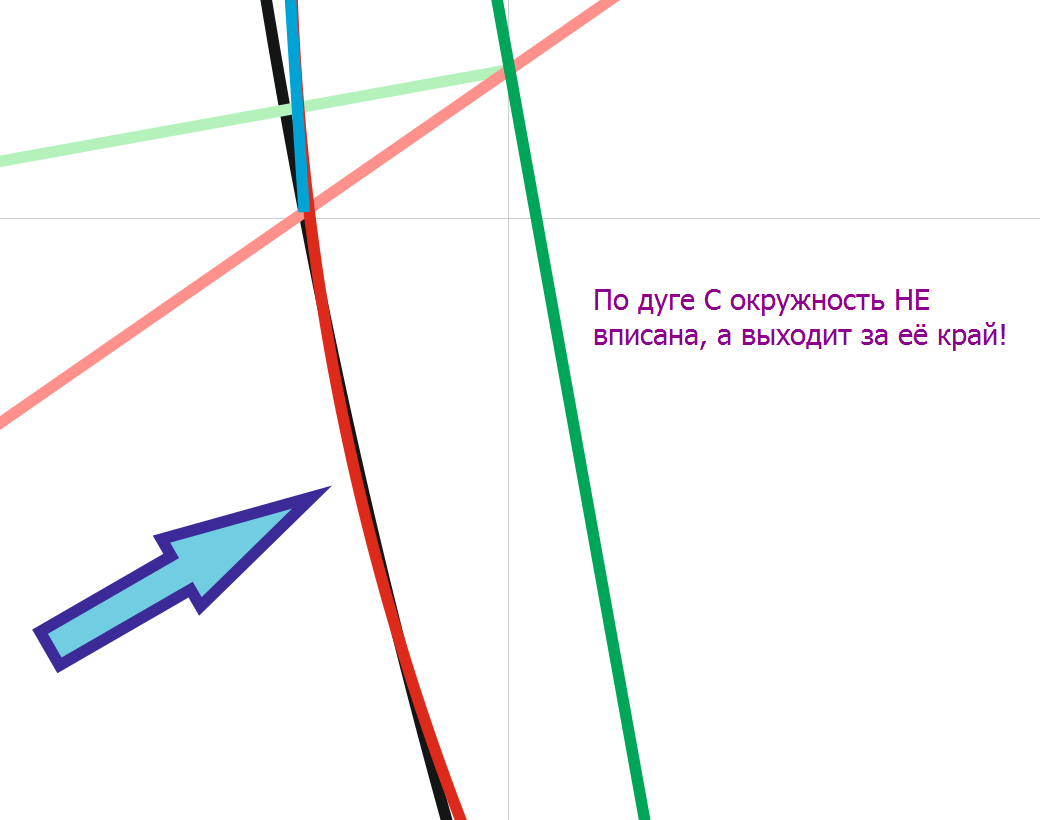
Но это не точно... Не точно в части вписания окружности в дугу C. Дуга окружности свешивается за край дуги C.
Это построение можно видеть на приложенных скриншотах.
Откуда можно понять, что по сторонам A, B окружность вписана, а вот на дуге C - окружность свешивается за край дуги C. И расхождение составляет 0,06 мм (при диаметре вписанной окружности 34,18 мм). Это также продемонстрировано.
То есть, то, что сделал я - это лишь приближённое, погрешное решение. Близкое к правильному, но точно не на 100 %.
Отсюда вопрос: как геометрически правильно вписать окружность в данную фигуру? А точнее, как найти эту точку на дуге C, к которой мы сможем провести отрезок E?
Мои мысли:
На самом деле голубой отрезок Е должен простираться до центра области перехлёстного наложения дуги C и окружности друг на друга. Тогда биссектриса от отрезка Е, точнее, от нового угла ЕА и будет находить точный центр относительно дуги С.
Т. е. если отрезок Е продлить дальше, до центра области перехлёстного наложения дуги C и окружности друг на друга, то угол между отрезком Е и стороной А будет меньше, следовательно, и точка пересечения (центр будущей вписанной окружности) двух биссектрис будет математически и физически дальше от дуги С. И тогда окружность будет вписана и в дугу С.
Также посетила мысль, что нахождение этой точки - это что-то из области графика убывающей функции f(x)...
***
***

***
***

***

***
***







