Определение местоположения множества векторов во множестве точек?

Question

[Дмитрий Петров]

Добрый день всем. Тема больше математическая, все равно.

В общем, есть некоторое пространство точек. К примеру, карта предметов на полу — на полу лежит штук 20 кубиков, известно точное расположение каждого из них.

В некоторой точке (x, y) этой комнаты находится наблюдатель (Н). Наблюдатель не знает своих координат в комнате. Наблюдатель знает свой угол поворота относительно оси север-юг.

Наблюдатель видит 5 кубиков, измеряет точное расстояние до каждого из них. Таким образом, наблюдатель получает набор векторов от себя до каждого увиденного кубика, знает длину каждого вектора.


Вопрос: Как наблюдателю определить свои координаты (X, Y), пользуясь известными данными о положении ВСЕХ кубиков комнаты, имея набор векторов? При этом наблюдатель не знает, какие кубики он видит (не знает номера кубиков, т.е. он не может точно определить, какой вектор на какой кубик указывает).


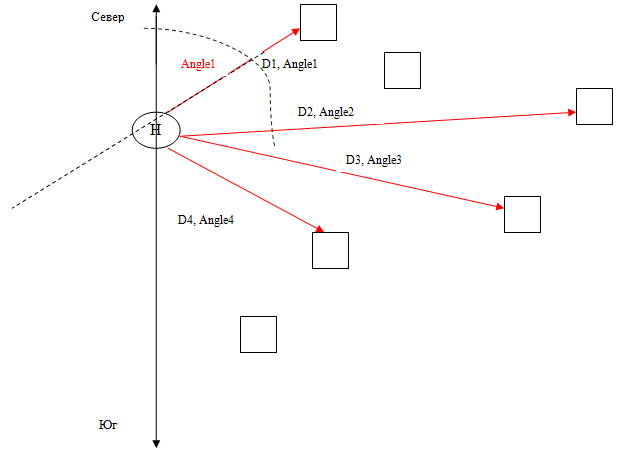
UPD1: Ниже привел картинку, иллюстрирующую ситуацию. Кубики — это известные точки, D₁-D_x — измеренные расстояния от наблюдателя (Н) до точек. Angle₁-Angle_x — углы поворота вектора относительно оси Север-Юг.

UPD2: Теоретическая задача — нахождение местоположения Н (наблюдателя) при известных D_x, Angle_x, известных координатах каждой точки.

Момент1: Наблюдатель не знает, до каких именно точек он измерил расстояние (не знает их глобальные координаты), ему известно только их расположение относительно себя (локальные координаты в координатной системе с наблюдателем в качестве центра.

Момент2: Все измерения проводятся в двумерной системе координат (в трехмерной мат.затраты будут слишком большие).


Картинка:



Практическая задача — нахождение местоположения робота в помещении. Известна карта помещения (координаты всех точек препятствий на высоте расположения датчиков робота), получены результаты измерений (лазерным датчиком линии или путем нескольких точечных измерений обычным сенсором с изменением угла поворота сенсора), надо определить свое положение. Задача осложняется тем, что точек в карте помещения (даже с учетом низкого разрешения, т.е. 1 точка на 10см, например) будет очень много, простой перебор всех вариантов займет некислое время.


Какой вариант возникал у меня:

1) Вычисление всех возможных относительных векторов от каждой точки до каждой точки карты (с учетом расстояния, т.е. вычисляем вектора только для точек, расстояния между которыми не больше метра). Назовем их глобальными векторами.

2) Вычисление всех возможных векторов между измеренными точками (мы знаем их координаты в локальной системе координат, можем вычислить относительные вектора. Назовем их измеренными векторами.

3) Перебор измеренных векторов.

3.1) Находится любой совпадающий глобальный вектор для измеренного вектора (совпадают направление и длина), фиксируется.

3.2) Выбирается следующий измеренный вектор, вычисляется его положение относительно предыдущего измеренного, затем идет поиск глобального вектора, расположенного так же относительно предыдущего фиксированного глобального.

3.2.1) Если глобальный вектор найден, то он фиксируется, переходим к шагу 3.2

3.2.2) Если глобальный вектор НЕ найден, результаты сбрасываются, переходим к шагу 3.1.

3.3) Когда все измеренные векторы перебраны и найдена комбинация глобальных векторов, соответствующих измеренным, то вычисляем координаты измеренных точек на основе найденных глобальных векторов.

3.4) Ну а вычисление точки расположения наблюдателя, когда известны координаты измеренных точек — это уже простая геометрия.

Comments

[Eddy_Em]

Автор, пожалуйста, уточните задание.
Все-таки, задача очень интересная, но из ваших комментариев не вполне понятная.

[Дмитрий Петров]

обновил основной пост :) с уточнениями

[Mrrl]

Вопрос по ситуации с «миллионом точек». Есть ли там ограничения на то, в какой (по размерам) области могут оказаться видимые кубики? Можно ли для каждого кубика перечислить те, которые могут быть видимы одновременно с ним?

[Дмитрий Петров]

область определяется характеристиками сенсоров. Разумный предел измерения — до метра от робота до препятствий. Плюс еще надо сделать измерения с разным углом поворота, а это сегмент круга шириной градусов 45-60.

Answer 1

[Eddy_Em]

Если кубиков достаточно много и расположены они достаточно хаотично, то на основании только знания координат кубиков и векторов расстояний от наблюдателя до каждого кубика вполне можно определить координаты наблюдателя.
Примерную задачу я решал для определения поворота и сдвига изображения звездного неба.
Вот только сложность здесь достаточно высокая: нужно будет перейти в систему координат одного из кубиков, построить на основе векторов наблюдателя вектора положений всех остальных кубиков относительно данного, а затем уже путем перебора известных из положений кубиков относительных векторов произвести идентификацию.
В итоге мы сможем точно получить координаты наблюдателя.
Кстати, чем-то эта задача похожа на триангуляцию по GPS (вот только «кубики» в этом случае отождествлены заранее, но вместо векторов мы имеем лишь длины).

Comments

[kreativf]

А разве результаты будут однозначными? Мне кажется что по 5 из 20 узнать определённые координаты трудно. Вот если знать углы между векторами, то всё было бы проще.
P.S. В триангуляции вы всё же всегда знаете с каким спутником вы общаетесь.

[Eddy_Em]

У меня проблема была в том, что часть объектов появляется, часть исчезает — т.е. перебирать иной раз приходилось довольно долго. А если количество кубиков постоянно, сложностей особых не будет.
Для полностью однозначного определения координат хватит (если считать погрешность нулевой) всего лишь трех кубиков — главное, чтобы они образовывали неравносторонний треугольник (точнее — все три стороны должны иметь разную длину).

В действительности мы имеем погрешность измерений, причем она зависит еще и от угла наблюдения — поэтому-то лучше, чтобы кубиков было побольше.
Относительные расстояния определяются с точностью до некоторой пороговой величины для каждого кубика, затем вычисляется некоторый критерий сравнения и по нему выбирается наиболее подходящая конфигурация. По ней и вычисляются расстояния.
Почитайте. Может, поможет.

[Mrrl]

Посмотрел. Похоже, что у меня такой же алгоритм )) :beer:

[Eddy_Em]

Вот так вот и рождаются велосипеды ☺

Answer 2

[Mrrl]

Я сейчас занимаюсь именно этой задачей. В данных условиях (небольшая база опорных точек и довольно точно известное положение нескольких из них в системе координат наблюдателя) ее можно решать так.

1 (предобработка). Для каждой точки из базы определяем расстояния до остальных 19 точек, полученный вектор сортируем. Получаем 20 векторов LB[20][19].
2. Для видимых точек делаем то же самое — получаем 5 векторов отсортированных расстояний LS[5][4].
3. Для каждой пары «вектор из LB / вектор из LS» определяем меру того, насколько второй вектор является подмножеством первого — для каждого элемента второго вектора ищем ближайший элемент первого и находим максимум или сумму отклонений.
4. Для каждого вектора из LS берем ближайший (в смысле заданной в (3) меры) вектор из LB. Получили первую кандидатуру на соответствие точек. Проверяем, соответствуют ли друг другу расстояния, и если да — пытаемся найти преобразование системы координат. Если видимые точки с хорошей точностью совпали с базой, то нам повезло.
Если не повезло, то дальше есть два пути.
5a. Начинаем просматривать не наилучшие соответствия, а следующие за ними (какой-нибудь динамикой). В конце концов повезет — у нас всего 5 индексов для перебора.
5b. Выбираем вектор из LS, соответствие которого с вектором из LB было наиболее надежным в том смысле, что второе по качеству соответствие (того же вектора из LS но с другим вектором из LB) гораздо хуже. Говорим, что самое надежное соответствие — правильное, т.е. один кубик мы узнали. Корректируем меру соответствий, добавляя новый критерий — расстояния до найденного кубика должны совпадать. После чего снова выбираем наиболее надежное соответствие, и т.д. Скорее всего, повезет.
Если не повезло, придется повышать сложность — например, сравнивать не расстояния между парами точек, а форму треугольников. Но я надеюсь, что до этого не дойдет.

Answer 3

[anmipo]

Ваша задача любопытна, кроме всего прочего, своей нетрадиционностью: известно точное расстояние до «кубиков», их точное положение, но между собой они неразличимы. Обычно в задачах позиционирования всё наоборот: известен ID станции (GSM cell ID, Wi-Fi MAC), но расстояние до неё можно только грубо прикинуть (по силе сигнала или времени его распространения), а где она находится — вообще непонятно.

Итак, входные данные: карта расположения кубиков, и набор из пяти расстояний x₁...x₅ до каких-то из этих кубиков (пусть с некоторой точностью ±Δ).

1. Берём карту, накладываем на неё прозрачный слой (в терминах графических редакторов).
2. Берём первое расстояние из набора, x₁ и вокруг каждого кубика на карте рисуем сплошное кольцо с внутренним радиусом x₁-Δ и внешним x₁+Δ.
   Кольца представляют множество всех возможных положений пользователя на основе одного измеренного расстояния.
3. Накладываем ещё один слой, рисуем кольца для x₂±Δ.
4. Производим объединение этого слоя с предыдущим, используя операцию AND, — то есть находим пересечение множеств. Результат будет множеством возможных положений пользователя с учётом двух измеренных растояний.
5. Повторяем шаги 3-4 для x₃...x₅.
6. Получившееся изображение показывает возможные положения пользователя с учётом пяти измеренных расстояний. Вполне вероятно, что таких положений будет несколько — значит, задача не имела однозначного решения. Не исключено также, что результат будет пустым множеством, — в таком случае стоит увеличить значение Δ.

Разумеется, расчёт пересечения колец — занятие не особо быстрое. Поэтому каждое кольцо можно заменить парой квадратов (вписанным и описанным) — и вся задача сведётся к поиску пересечений прямоугольников. А это даже микроконтроллер посчитает за десяток тактов :)

Comments

[Дмитрий Петров]

очень интересное решение, завтра попытаюсь реализовать)

[Eddy_Em]

Если у нас 20 кубиков и 5 расстояний, то аналитическое решение этой задачи таким способом будет сложноватым.

[Mrrl]

Любопытно. Решение совершенно не учитывает направлений — только расстояния. Обычно направления известны точнее. Если только наблюдатель — не летучая мышь :)

[Mrrl]

Аналитическое решение совсем просто: сначала находим по двум расстояниям не более 760 возможных положений, потом проверяем их на корректность :)

[anmipo]

Eddy_Em, так на то и компьютеры, чтобы не решать аналитически. Для 20-и кубиков и 5-и расстояний нужно будет только 4 раза посчитать пересечения 40+40 квадратов.

Mrrl, да, мне кажется, что в этой задаче направление взгляда пользователя не очень помогает: когда на входе только «три метра», кубик может быть и спереди, и сзади, и сверху, — мы можем только сказать, что он находится где-то на трёхметровой сфере вокруг пользователя-точки :)

[Mrrl]

Зато помогает угол между направлениями на два кубика. Сразу дает расстояние между ними.

Answer 4

[lashtal]

Это обычная задачка при совмещении перспективы камеры и 3д сцены. Camera matching.
Да, нужно 5 известных точек (кубиков) для вычисления коорд. наблюдателя, но, желательно, чтобы они не лежали в одной плоскости. В блендере или скриптах для него должна быть реализация, я бы туда копал.

Answer 5

[Mrrl]

А, кстати, если известны и относительные координаты маяков, и направление север-юг, то все вообще просто. Для каждой пары «маяк из базы — видимый маяк» вычисляется наше положение для случая, если они соответствуют друг другу, после чего в полученном облаке из 100 точек определяется самый плотный 5-точечный кластер (за последнее время задача обсуждалась здесь по меньшей мере трижды).

Answer 6

[Дмитрий Петров]

Реализовал алгоритм, предложенный DankoUA в этом посте. Заработало сходу с первого раза, что слегка сбило с толку) Определяется положение очень быстро, растет, естественно, пропорционально количеству точек на карте, но это без оптимизаций. Точность — 95%. Я что-то слегка в дауне — впервые реализованный алгоритм работает с первой попытки и выдает точные результаты)

Answer 7

[kreativf]

Если он не знает какой вектор указывает на какой кубик, то по моему у него нет привязки к координатам кубика и следовательно он не может определить своё местонахождение.

Answer 8

[Дмитрий Петров]

Может. Можно вычислить множество всех возможных комбинаций и в итоге получить нужное, но цена этого алгоритма даже не O в степени N, а что-то похлеще. Есть подобные алгоритмы в математике, но вспомнить не могу…

Answer 9

[Дмитрий Петров]

углы не проблема. Векторы известны — известно направление и расстояние. т.е. можно определить угол между векторами, ведь они все начинаются в одной условной точке (0,0) относительно наблюдателя.

Comments

[kreativf]

Тогда вы сможете по углу и длинне векторов определить расстояния между нужными кубиками и после этого вычислить ваше местоположение. Тогда 5 кубиков это больше чем нужно.

[Mrrl]

5 кубиков — в самый раз. Между 20 кубиками 190 разных расстояний, среди которых наверняка окажутся близкие — нам может сильно не повезти.

[kreativf]

Зависит от того говорим мы о 2д или о 3д пространстве.

[Eddy_Em]

Нужно замерять расстояния между кубиками не в декартовой, а в полярной системе координат. Тогда, сортируя по модулю радиус-вектора, получим для каждого кубика свою уникальную конфигурацию. Ну, а разные угловые координаты не дадут нам «перепутать» близкие по модулю расстояния.

[kreativf]

> карта предметов на полу — на полу лежит штук 20 кубиков
Это же в принципе 2д

[Mrrl]

Не зависит. 2d и 3d тут различаются мало. А «расстояния в полярных координатах»(не знаю, правда, что это такое) не инварианты относительно перемещения в пространстве, поэтому не помогут. Чтобы спастись от близких координат, можно искать треугольники — им совпасть сложнее, и при 20 опорных точках их немного (всего 1140). Мне хуже, у меня точек 150 :(

[Mrrl]

Да, не заметил, что наблюдатель тоже в 2D — решал для 3D :D

[Дмитрий Петров]

точек вообще может оказаться под миллион, основная задача, для которой нужно это решение — определение местоположения по данным датчиков расстояния. при известных картах помещений.

[Mrrl]

То есть, направления неизвестны? Тогда, конечно, только метод «колец». Другой вариант: берем два сигнала (с наименьшими расстояниями), перебираем все пары точек, расстояние между которыми допустимо (лежит между суммой и разностью измеренных), строим два возможных положения наблюдателя, и для каждого проверяем — есть ли точки на трех остальных расстояниях. Проблема в том, что если наблюдатель оказался между двумя датчиками, его положение определяется слишком неточно.

[Eddy_Em]

Датчики расстояния уже пронумерованы. Но они не определяют направление. Надо было об этом сказать.
У вас уже классическая задача спутниковой навигации получается. Решается аналитически по (минимум) трем показаниям датчиков расстояния.

[kreativf]

> Векторы известны — известно направление и расстояние. т.е. можно определить угол между векторами
Автор же вроде сказал что известны и направление и расстояние.

[Mrrl]

Вроде сказал. А потом прозвучали «датчики расстояния». Если это мишени, промеренные лазерным теодолитом, то это одна задача. Если сигналы, полученные роботом от маяков — другая. Есть и третья: известны и направления и расстояния, но неизвестно, как они связаны друг с другом :)

[kreativf]

Автор, уточните пожалуйста задание, интересно же!

[Дмитрий Петров]

:) Уточню — есть неподвижный наблюдатель. У него есть средство измерения расстояния до препятствий. Наблюдатель знает свой угол поворота относительно оси «Север-Юг».
Соответственно наблюдатель может измерить расстояние от себя до определенной точки, при этом он знает собственный угол поворота и может определить направление от себя до точки (например, условно говоря — «строго вниз 300 миллиметров» или «400 миллиметров на 3 часа — 45 градусов»)

[Eddy_Em]

И еще уточнение: наблюдатель таки в 3D движется?
Хотя, в принципе, особого значения это не имеет при условии, что все опорные предметы расположены строго в одной плоскости.

Answer 10

[Дмитрий Петров]

придется делать m проверок на принадлежность, беря за отсчет последовательно каждую точку сетки. А еще не стоит забывать про нечеткость — проверка не должна быть точной, надо делать допуск

Comments

[Дмитрий Петров]

то есть если я правильно понял DankoUA, вы предлагаете составить сетку из всех точек карты, далее сделать маленькую сетку из измеренных точек и двигать её по большой сетке, последовательно примеряя на совпадение?

Answer 11

[Mrrl]

В случае, если векторов между потенциально видимыми кубиками не безумно много (например, если на карте много комнат, но в каждой комнате не очень много кубиков), то всю задачу можно решить быстрее, чем за O(n). Берем равномерную сетку, но помещаем в нее не координаты кубиков, а вектора между ними (номера двух кубиков и вектор). Скорее всего, даже хеширования не понадобится — будет плотно заполненный двумерный массив списков. Берем любой вектор между двумя видимыми кубиками, находим соответствующий ему список векторов между кубиками базы, и идем по нему. Для каждой пары из списка находим положение наблюдателя и выполняем шаги (6,7) из алгоритма DankoUA (т.е. сетка с кубиками нам тоже понадобится).

Answer 12

[Eddy_Em]

Так как нам известна ориентация обеих систем координат (т.е. направление «север-юг»), задача существенно упрощается.
Могу предложить такие варианты:

1. Геометрический — посредством кросс-корреляционной функции (ККФ). Суть его в следующем: координатная сетка положений датчиков квантуется по какому-то определенному уровню и каждый датчик на ней представляется одним пикселем. Получаем базовое изображение. Исходя из измерений наблюдателя мы получаем аналогичное (но маленькое) изображение — эталон. Эталон по сути является частью базового изображения. Нам остается найти положение эталона на базовом изображении. А для этого мы строим ККФ и по ее максимуму с точностью до кванта расстояния получаем смещение наблюдателя. Уточнить его — уже простейшая задача.
Этот вариант будет тем более выгодным, чем больше точек мы имеем (т.к. он зависит не от количества датчиков, а от их размещения).

2. Аналитический. Этот вариант сильно зависит от количества датчиков. Пусть N — общее количество датчиков, а M — количество датчиков, замеченных наблюдателем.
2а. Сначала — найти расположение двух случайно выбранных точек из обнаруженных датчиков на общем поле (таких положений может быть несколько == k); затем — перебором отождествить остальные точки, чтобы однозначно определить, что за датчики засек наблюдатель. Здесь можно как «тупо» перебирать все вектора, выбрав одну из точек в качестве базы, так и пойти по другому пути: «вырисовать» произвольный векторный «рисунок», проходящий через все обнаруженные точки (так, чтобы каждая точка была соединена с одной или двумя соседними), затем пробежаться по всем N точкам в поисках первого подходящего совпадения (т.е. если сумма положения i-й точки и 0-го вектора «рисунка» даст положение другой точки, считаем, что совпадение найдено), далее, подставляя 1-й вектор к найденной второй точке, ищем третью. Если она найдена — ищем далее. Нет — продолжаем перебор в поисках 0-го вектора. А можно сделать «рисунок», так же взяв за основу одну из найденных точек, но проводя вектора к остальным точкам от нее. Это уменьшит погрешность округления координат (которая может давать ложные совпадения в случае прохода по «рисунку»-траектории).
2б. Заранее построить упорядоченные (скажем, по углу или по расстоянию) массивы положений (в полярной СК) датчиков друг относительно друга. Получим N массивов из (N-1) векторов. По обнаруженным датчикам строим аналогичный массив, но один: взяв за опорную любую из обнаруженных точек. Далее нам нужно лишь сравнить наш массив из (K-1) векторов с N массивами.
Эту операцию можно ускорить, если опять-таки провести квантование (скажем, по углу): мы строим N псевдогистограмм, допустим, с шагом по 10 градусов (получится псевдогистограмма из 36 «столбцов), каждая ячейка псевдогистограммы будет массивом длин векторов, имеющих угловую координату в данном интервале или NULL, если таковых нет. В этом случае поиск будет иметь сложность где-то O(KN). Но для однозначности требуется строгая неравномерность распределения датчиков.

Comments

[Eddy_Em]

В случае 2б s/K/M/g