Как считать по модифицированной формуле Жаккара?

Question

[HitGirl]

Здравствуйте!
В данной статье есть заголовок: "метод ассоциаций".

Там указана данная формула:
$$\operatorname{sim}_\text{ассоциаций}(X,Y)=\frac{\frac{|X \cap Y|}{|X|}}{\frac{|\bar{X} \cap Y|}{|\bar{X}|}}$$

Я попробовал посчитать по ней схожесть двух пользователей. Допустим в каталоге всего 5 товаров $i_1, i_2, i_3, i_4, i_5$

Обозначим множеством $X$ все фильмы купленные первым пользователем (первые два фильма): $X=\lbrace i_1, i_2 \rbrace$, тогда $\bar{X}=\lbrace i_3, i_4, i_5 \rbrace$

Обозначим множеством $Y$ все фильмы купленные вторым пользователем (второй и четвёртый фильм): $Y=\lbrace i_2, i_4 \rbrace$

Подставим значения в формулу:

$$\operatorname{sim}_\text{ассоциаций}(X,Y)=\frac{\frac{|X \cap Y|}{|X|}}{\frac{|\bar{X} \cap Y|}{|\bar{X}|}}=\frac{\frac{|\lbrace i_2 \rbrace|}{|\lbrace i_1, i_2 \rbrace|}}{\frac{|\lbrace i_4 \rbrace|}{|\lbrace i_3, i_4, i_5 \rbrace|}}=\frac{\frac{1}{2}}{\frac{1}{3}}=1,5$$

Подскажите, пожалуйста, правильно ли я вычислил схожесть, в каких диапазонах лежит схожесть по этой формуле? как эта формула называется на английском?

Comments

[Максим Припадчев]

К сожаление сайт не рендерит latex. Так что не понятно, ничего.

Answer 1

[Rsa97]

Берём формулу и рассматриваем крайние случаи.
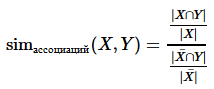Первый крайний случай - подмножества совпадают, X ≡ Y и X ≢ ∅. В этом случае числитель дроби будет равен единице (X ∩ Y ≡ X => |X ∩ Y| = |X|), знаменатель равен нулю (|X̅ ∩ Y| = 0). Соответственно, результат будет +∞.
Второй крайний случай - подмножества не содержат одинаковых элементов, X ≢ ∅, Y ≢ ∅. В этом случае числитель равен нулю (X ∩ Y ≡ ∅), в знаменателе |Y| / |X̅|. Соответственно, результат будет 0.
Особые случаи - X ≡ ∅, Y ≡ ∅, X̅ ≡ ∅.