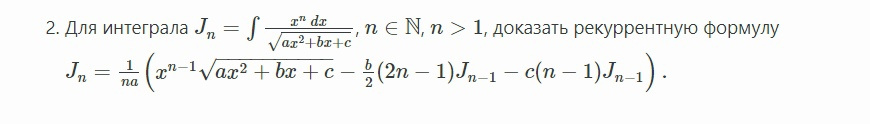В задаче опечатка, там где-то должно быть J(n-2) вместо J(n-1), и в коэффициентах я не уверен.
По идее в таких интегралах надо интегрированием по частям выводить рекуррентную формулу. Посмотрите на ответ - интеграл равен функции минус какой-то еще, похожий на изначальный, интеграл. Именно так и выглядит интегрирование по частям.
Осталось поэксперементировать перебирая разные части x^n и корня из квадртатного выражения: что из них интегрировать, а что дифференцировать.
Интегрировать корень в знаменателе будет очень тяжко, там логарифмы какие-нибудь вылезут и вообще форма выражения будет совсем другой. Попробуйте продифференцировать 1/sqrt(), а оставшеюся часть интегрировать. Или можно домножить числитель и знаменатель на корень, тогда корень можно уже интегрировать, а оставшееся рациональное полиномиальное выражение дифференцировать.
Еще можно с конца идти - перенесите все интегралы в одну сторону, сгрупируйте. Получите интеграл равен функции. Можно проверить равенство просто продифференцировав функцию.
Похоже в задании опечатка - там должны быть J(n-1) и J(n-2), потому что дифференцируя вот эту свободную штуку получается (C1x^n+C2x^(n-1) + C3x^(n-2)) / sqrt(ax^2+bx+c). Значит, с другой стороны должны быть линейная комбинация J(n), J(n-1) и J(n-2).