Как решить многокритериальную задачу о назначениях?

Question

[yggthris]

Мне нужно решить аналог многокритериальной задачи о назначениях, но есть ключевая деталь - на "должность" могут быть назначены несколько человек.
По сути - есть субъекты Zi; есть параметры, по которым они оцениваются - Yi. И есть нечёткие значения - низкая совместимость, средняя, и высокая - это Xi, но на деле их пять. Для каждого субъекта нужно определить уровень совместимости по Yi критериям.
Очень похоже на то, что есть в этой статье, но по итогу значения получаются неудовлетворительными.
Покажу в картинках. Вот наборы значений:

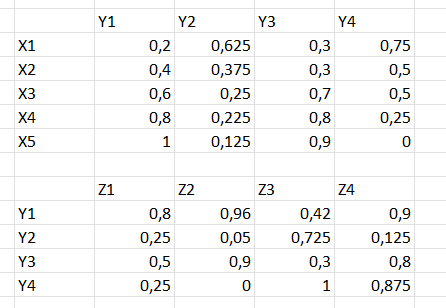
Вот (min-max)-композиция:

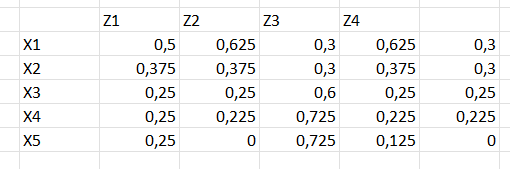
Вот (max-prod)-композиция:

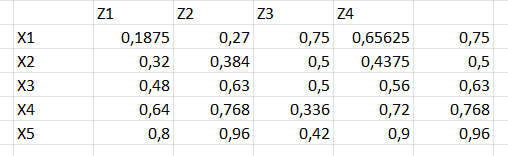
И в итоге результаты примерно схожие, но неудовлетворяющие. Что-то вечно не так с Z4 - 0,875 по Y4 - это очень плохой результат, а если я меняю Y3 на 0 - что тоже очень плохо - ничего не меняется.
Мне нужно получить результат наподобие: Z1 - X4, Z2 - X5, Z3 - X1, Z4 - X2, но это просто пример.
Также я пробовал сделать что-то по этой статье, результат хороший, но я слабо понимаю алгоритм в конце и не уверен, что правильно интерпретирую данные. Имеет ли вообще смысл использовать его для моих данных?
В целом - может есть какие-то другие рекомендации по многокритериальной задаче о назначениях? Я смотрел англоязычные источники, но там полно платных статей, да и я не вижу пользы искать где-то к ним доступ, если не знать, что ищешь.

Comments

[Wataru]

Какой смысл у этих Y? Типа какие-то произвольные параметры людей и работ? Например, физическая сила, ум, выносливость? Или как много в каждой работе определенного действия и как хороши люди в них?

[yggthris]

Wataru, это вообще не про параметры работ, я говорю про задачу о назначениях потому, что она очень похожа на мою. Если это правда важно, то Z - резюме, Y - различные параметры, которые могут помочь определить то, насколько работодателю подходит это резюме(процент совпадения навыков в резюме с навыками в вакансии, расхождение в опыте в резюме и в вакансии и так далее).

[Wataru]

ajdivot, стоп, у вас тут 2 таблицы Z-Y и X-Y. Что тогда X?

[yggthris]

Wataru, X - то, насколько резюме подходит работотаделю. Высокая, средняя, низкая совместимость. И промежуточные значения.

Answer 1

[rPman]

Строки - работники, колонки - критерии?
В общем случае тебе нужно составить метрику, самая тупая - это расстояние в евклидовом пространстве до нулевой точки - т.е. квадратный корень из суммы квадратов значений (в твоем случае критериев)

Если нужно сравнивать двух работников, то тогда квадратный корень из суммы квадратов разностей их критериев, но осторожно, эта метрика не транзитивна, т.е. если работник A лучше B, а B лучше C, то A не обязательно будет лучше C.

В некоторых случаях каждый критерий дополнительно умножают на коэффициент значимости (на сколько критерий сильно влияет на итоговое значение метрики, например длина волос для офисного сотрудника не самый значимый критерий и коэффициент у этого критерия ниже чем умение работать за компьютером), особенно это актуально когда критерии не нормализованы (не находятся на одном и том же интервале, например 0..1).

Предполагается что критерии имеют одинаковый смысл - чем больше значение тем лучше, так же рост значимости - линейный, т.е. увеличение значения критерия в два раза и в четыре означает буквально улучшение в 2 раза и в 4 соответствено. Бывает, когда значение критерия обратное и не ограничено, т.е. чем меньше тем лучше, тогда его переворачивают 1/(X+1) в этом случае значение критерия станет на интервале 0-1 (правда не линейное но это более сложный разговор, к примеру экспоненту в линейный превращают логарифмом)

Итого формула: Xi=sqrt(SUMj((Aj*Yij)^2))
Где i - номер строки, j - номер колонки, Xi - значение метрики для i-го работника, Yij - значение критерия j для работника i, Aj - коэффициент значимости критерия j

upd. существуют другие алгоритмы, например - критерии сортируются по убыванию значимости, сначала сотрудники сортируются по важнейшему критерию, берется некоторое их количество сверху (например половина), и сортируются по второму по значимости критерию, берется некоторое их количество (от остатка первого критерия) сверху и так далее. Этот способ подходит когда значения критериев дискретны (вырожденный случай - да/нет, т.е. к примеру знает ли работник язык программирования, женщина ли с риском уйти в декрет и т.п.)

Скорее всего придется сочетать эти алгоритмы, т.е. сначала исключить работников, которые в принципе не соответствуют критериям (зачем тебе программист, не умеющий программировать) а затем оставшихся выбирать по метрике выше