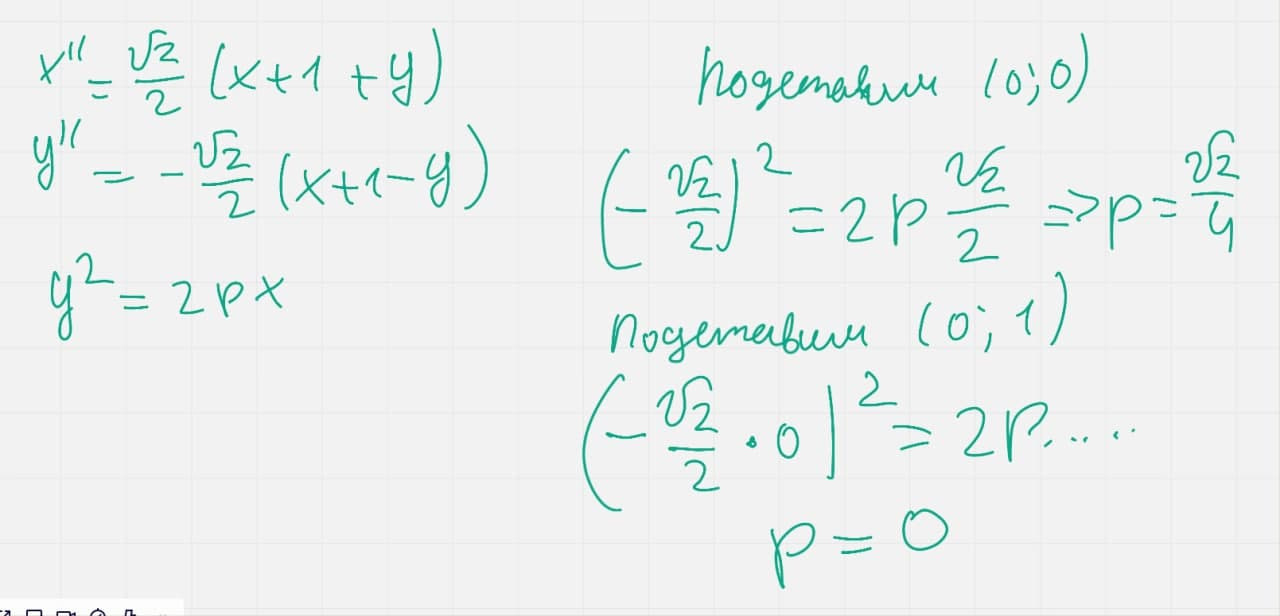1. Сместим систему координат вниз на 1.
x' = x
y' = y + 1
Обратное преобразование:
x = x'
y = y' - 1
Уравнение прямой: y = x − 1, y' − 1 = x' − 1, y' = x'
Переход точек: (0, 0) → (0, 1), (0, 1) → (0, 2)
2. Повернём систему координат по часовой стрелке на π/4.
x'' = x'⋅cos(π/4) − y'⋅sin(π/4) = x'⋅√2/2 − y'⋅√2/2
y'' = x'⋅sin(π/4) + y'⋅cos(π/4) = x'⋅√2/2 + y'⋅√2/2
Обратное преобразование:
x' = x''⋅cos(π/4) + y''⋅sin(π/4) = x''⋅√2/2 + y''⋅√2/2
y' = −x''⋅sin(π/4) + y''⋅cos(π/4) = −x''⋅√2/2 + y''⋅√2/2
Уравнение прямой: y' = x', x''⋅√2/2 + y''⋅√2/2 = −x''⋅√2/2 + y''⋅√2/2, x'' = 0
Получили, что прямая стала осью ординат.
Переход точек: (0, 1) → (−√2/2, √2/2), (0, 2) → (−√2, √2)
Уравнение параболы, симметричной оси ординат: y'' = a⋅x''2 + b
a/2 + b = √2/2
2⋅a + b = √2
Отсюда a = √2/3, b = √2/3
y'' = √2/3⋅x''2 + √2/3
x'⋅√2/2 + y'⋅√2/2 = √2/3⋅(x'⋅√2/2 − y'⋅√2/2)2 + √2/3
x'2 + y'2 − 2⋅x'⋅y' − 3⋅x' − 3⋅y' + 2 = 0
x2 + (y + 1)2 − 2⋅x⋅(y + 1) − 3⋅x − 3⋅(y + 1) + 2 = 0
x2 + y2 − 2⋅x⋅y − 5⋅x − y = 0