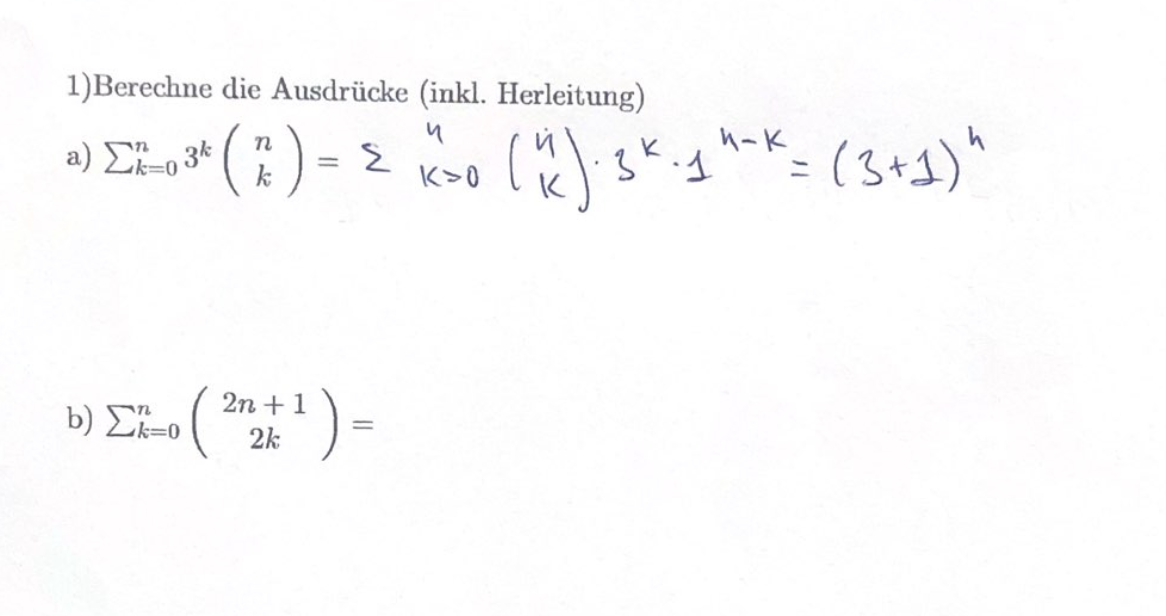В моей нотации С(n,k) - сочетания из n по k.
Нужно знать вот это тождество для сочетаний:
С(n,k) = C(n,n-k).
Применив к тому, что у нас под знаком суммы:
C(2n+1, 2k) = С(2n+1, 2n+1-2k)
Когда k проходит от 0 до n, слева получаются сочентания по всем четным числам от 0 до 2n+1, а справа - по всем нечетным.
Есть формула, что сумма всех сочетаний из n по всем возможным k будет 2^n, Получается тупо из раскрытия (1+1)^n по биному Ньютона.
Но у нас тут не сумма по всем, а только по четным. Но выше мы уже видели, что суммы по всем четным и всем нечетным совпадают. Отсюда напрашивается варинат просто подсчитать удвоенную искомую сумму.
Формально: пусть X - искомая сумма в задаче.
тогда
X+X = sum_{k=0..n} C(2n+1, 2k) + sum_{k=0..n}(2n+1, 2n+1-2k) =
= sum_{k=0..n} C(2n+1, 2k) + sum_{k=0..n}(2n+1, 2*(n-k)+1) =
= sum_{k=0..n} C(2n+1, 2k) + sum_{k=n..0}(2n+1, 2*(n-k)+1) =
Во второй сумме заменим n-k=j. Т.к. k=n..0, то j = 0..n.
= sum_{k=0..n} C(2n+1, 2k) + sum_{j=0..n}(2n+1, 2*j+1).
А это тупо сумма по всем возможным k от 0 до 2n+1 (только четные и нечетные в отдельных суммах):
= sum_{k=0..2n+1} C(2n+1, k) = 2^(2n+1)
Остюда X = 2^(2n+1) / 2 = 2^(2n)