Прошу помощи в выборе формулы для описания поверхности распределения вероятности.
Основная сложность – как основу можно использовать различные типовые формулы – парабола, гипербола, синусоида, сфера и т.д.
Поверхность распределения вероятностей будет иметь вид, аналогичный изображению на приложенной картинке:
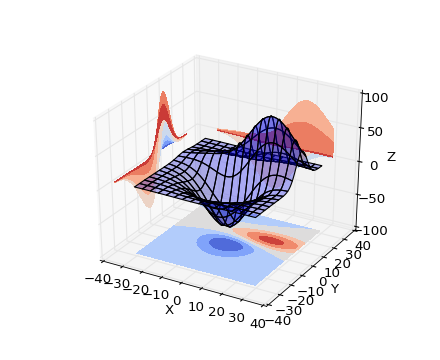
Т.е. всегда будут у поверхности минимум два пика – положительный и отрицательный. Они могут отличаться по высоте и расположению. С каждой стороны осей X и Y могут быть свои отрицательные и положительные пики.
Для расчета вероятности используем Байесовскую вероятность, т.е. мы имеем возможность учитывать ожидание наступления события
Опыт имеет следующий вид (для классического примера с подбрасыванием монетки):
1. Есть гора (склон горы) в основании которого находится бетонный блок. Это "Установка по запуску монетки".
2. Есть вагонетка, которая скатывается по склону и упирается в бетонный блок. Это "Монетка".
Условия опыта:
Вагонетка ВСЕГДА упирается в бетонный блок.
Вагонетка может остановиться о бетонный блок и при этом не получить повреждений - это "Положительный пик" поверхности.
Вагонетка может остановиться о бетонный блок и полностью разрушиться - это "Отрицательный пик" поверхности.
Вагонетка может остановиться о бетонный блок и разрушиться частично - это иные значения поверхности.
С периодичностью 1 сек. рассчитываем вероятность (т.е. подбрасываем монетку) успешной/неуспешной/частично успешной остановки Вагонетки о бетонный блок.
При нулевом шаге испытаний, т.е. до первого броска монетки, Испытатель может выбрать склон горы, его крутизну, профиль рельефа, размер и т.п.
В процессе испытаний повлиять на "Установку по запуску монетки", т.е. "Гору" испытатель не может, либо его влияние стремиться к нулю и им можно пренебречь. Какое-либо влияние на "Установку по запуску монетки" Испытатель может оказать ДО испытаний, выбрав параметры.
Испытатель может влиять на физические характеристики Монетки/вагонетки таким образом, чтобы максимально приблизиться и в процессе всего испытания, находиться в районе положительного пика.
Т.е. спускаясь с Горы Испытатель может менять характеристики движения вагонетки (тормозить, наклонять, разгонять и иным образом влиять) и при этом его основная цель - остановиться с минимальными повреждениями.
Т.к. основная задача остановить вагонетку с наименьшими повреждениями, то действия Испытателя подвержены именно этой задаче. Соответственно, если в результате действий Испытателя параметры сдвигаются в сторону отрицательного пика, то его действия должны быть направлены на изменение Монетки/вагонетка таким образом, чтобы сдвинуться в сторону положительного пика, но эти действия могут не увенчаться успехом.
-------------
Вот для такого опыта мне нужно построить поверхность распределения вероятностей.
Как примерно должна выглядеть поверхность распределения вероятностей – я указал в самом начале вопроса.
Какой вид формулы посоветуете – гипербола, парабола, синусоида (они при вращении дает конусы, которые могут представлять собой пики)? Или имеет смысл использовать уравнение сферы, рассеченной плоскостью осей XY и смещенные относительно друг друга?
P.S.: Можно предположить, что будут три вида изменяемых параметров - A-внутренние параметры системы, B - внешние параметры системы, C - управляющее воздействие Испытателя. Но это сугубо мои предположения...

