Комплексная вероятность. Как реализовать генерацию случайного коэффициента по графику?

Question

[Марк Березовский]

Я столкнулся с интересной задачей, на которую бы хотел иметь решение. Мне требуется получить случайное число по коэффициенту (min + abs(max - min) * coef), но не просто случайное число, случайность этого числа будет соответствовать графику. Допустим, чтобы рандом чаще всего выдавал коэфициент меньше 0.5, и реже больше 0.5. Я привел ниже иллюстрацию графика. Как такое можно реализовать? (Прошу приводить примеры в виде кода, или же в виде объяснения алгоритма)

Comments

[twobomb]

Ну что-то типа если допустим rand() < 0.8 то coef = rand(от 0 до 0.5), а если больше то rand( от 0.5 до 1), таким образом с вероятностью 80% коэфициент будет меньше 0.5, и с вероятностью 20% что больше 0.5. Ну можно сделать кучу проверок на определенные отрезки.

[Марк Березовский]

twobomb, да, ты понял задачу. но проверка идет не на отрезки, а по графику(или же массиву векторных точек: ~[0.9, 0.85, 0.67, 0.31, 0.05])

[Lynn «Кофеман»]

Пусть обычный генератор выдаёт случайные числа на отрезке [0, 1) равномерно. Тогда нужно всего лишь найти (подобрать) функцию которая преобразует этот генератор в то что нужно.
Например, возьёмём в качестве такой функции x², т.е. rand2() = pow(rand(), 2). Тогда с вероятностью 1/2 случайное число будет меньше 0.25, а не 0.5 как было изначально.

Т.е. ваша задача просто подобрать такую функцию.

Answer 1

[dmshar]

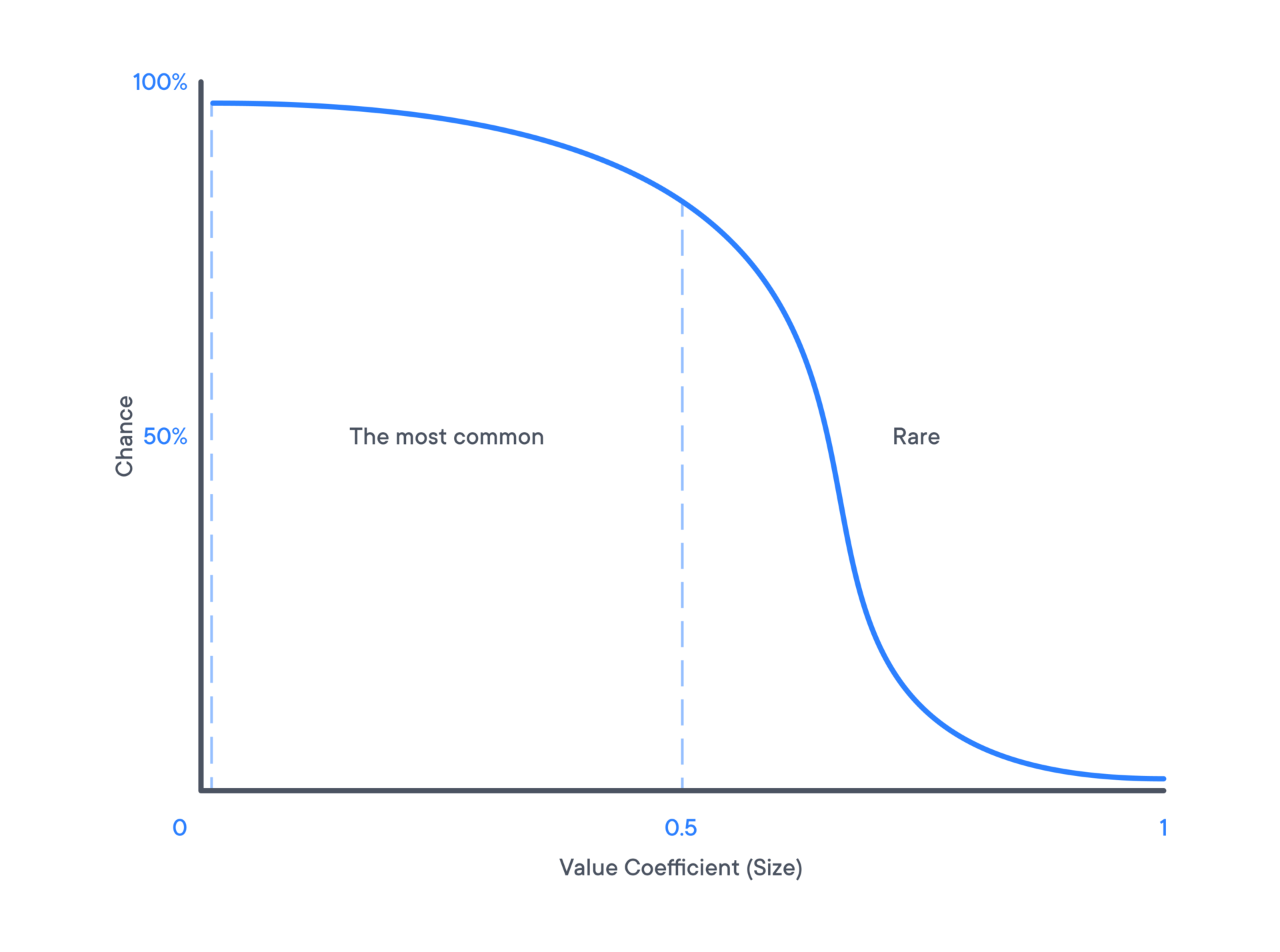
Все зависит от того, знаете-ли вы формулу вашей ф-ции (квази)плотности распределения. Надеюсь, что у=F(r) известна, и соответственно, известна и функция Ф(y)=r, обратная к ней. Тогда не надо изобретать велосипед, все придумано до нас.
Например: stratum.ac.ru/education/textbooks/modelir/lection2...
На пальцах:
Генерируете равномерно распределенное число в диапазоне от (по вашему рисунку) 0 до 100%. Получаете точку y на оси Y. Потом считаете r=Ф(y).Последовательность таких точек {r} будут генерироваться случайным образом, в строгом соответствии с вашим законом распределения.
Не просто "чаще"-"реже", и именно в соответствии с вашим законом.
Так поступают всегда и все. Реализация на Python - в три строчки.

Answer 2

[Марк Березовский]

Первый вариант решения - f(r()), где f = функция графика, r = функция рандома.
Второй вариант - найти проекцию случайной нормали [0, 1] оси x по оси y, но этот вариант менее точный.
Ниже приведена реализация второго варианта:

Answer 3

[xmoonlight]

случайность этого числа будет соответствовать графику.

Нужно составить полином этой зависимости. Т.е., сам этот график.

Допустим, чтобы рандом чаще всего выдавал коэфициент меньше 0.5, и реже больше 0.5.

Следующий шаг - это вероятность выпадения одного из параметров (по одной из 2-х осей).