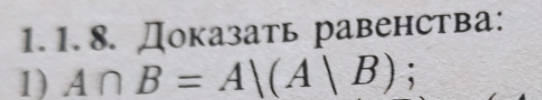Как доказать равенство множеств?

Question

[Anonymous85966]

1)При пересечении a и b x будет принадлежать как множеству а, так и множеству b.
2)При разности в правой части в скобках x будет принадлежать a и не будет принадлежать b.При еще одной разности множества a на скобку x будет принадлежать a и не будет принадлежать а и будет принадлежать b.
В чем проблема?Мне кажется, я не понимаю сам процесс раскрытия скобок в правой части

Answer 1

[AVKor]

Доказывать надо по определению равенства множеств.

Answer 2

[Wataru]

Формально по законам логики и определениям.
Что значит какой-то элемент принадлежит правому множеству?
x in A\(A\B), тогда и только тогда, когда x in A И x not in (A\B),
Чтобы вторая половина после И выполнялось, надо наложить отрицание не x in (A\B) что тоже самое, что (x in A И x not in B). По законам логики это будет (x not in A ИЛИ x in B). добавляем к этому первую часть и раскрываем скобки:

x in A И (x not in A ИЛИ x in B) = (x in A И x not in A) ИЛИ (x in A И x in B).

Первая часть - всегда ложна и сокращается, остается только (x in A И x in B), что по определению x in A и B. Мы везде использовали только эквивалентность и из определения, что элемент принадлежит правому множеству, получили определение, что элемент принадлежит левому множеству. Значит эти 2 множества равны.