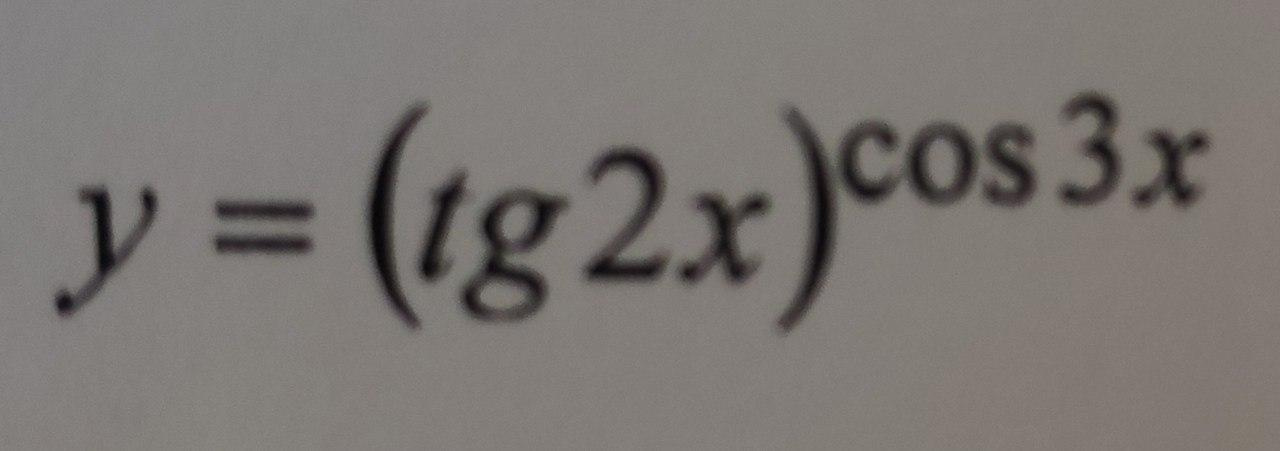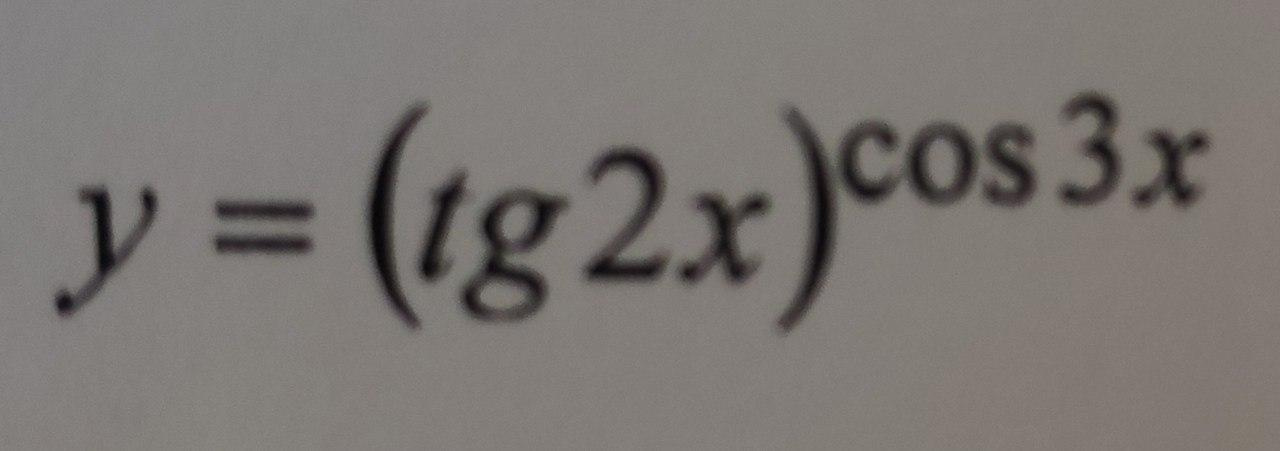
Я делаю так: сначала вычисляю производную (tg2x)`, у меня получилось 1/cos^2(2x),
после чего вероятно надо действовать по формуле a^x, но здесь я путаюсь и получается какая-то абракадабра.
Похожие задания не гуглятся, поэтому прошу помочь с решением.