A B !2A B&!2A R
0 0 1 0 0
0 1 1 1 1
1 0 -1 0 1
1 1 -1 -1 0


A B A-B
0 0 0
0 1 1
1 0 1
1 1 0A-B=A xor B, следовательно - := XOR.A B (Необщая часть A) (Необщая часть B) (Объединения частей)
0 0 0 0 1
0 1 0 1 1
1 0 1 0 1
1 1 0 0 0A B A-B
-1 -1 0
-1 0 -1
-1 1 -2
0 0 0
0 1 -1
1 0 1
1 1 0
A B A-B
0 0 0
0 1 1
1 0 1
1 1 0A-B=A xor B, следовательно - := XOR.A B (Необщая часть A) (Необщая часть B) (Объединения частей)
0 0 0 0 1
0 1 0 1 1
1 0 1 0 1
1 1 0 0 0
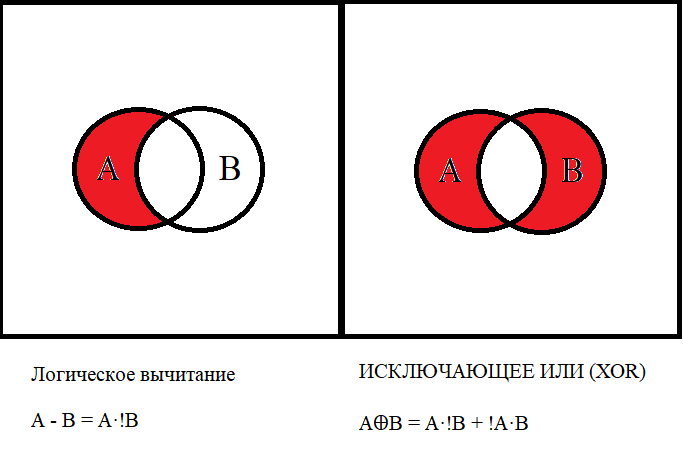

В булевой алгебре НЕТ вычитания и деления, поскольку это предполагало бы ответы для выражения 0-1=-1, а такого в бинарной системе быть не может.
-1 mod 2 = 1Учитывая, что А - В в булевой алгебре означать может только А·!В, то таблица истинности должна быть следующая:
Это обычное кольцо по модулю 2. Поэтому все простейшие операции естественным образом работают, в том числе и вычитание. -1 mod 2 = 1
Если вы говорите конкретно про алгебру логики, то в ней и 0, 1 тоже отсутствуют - есть только ложь, истина, клнъюнкция, дизъюнкция и отрицание.
Хотелось бы увидеть ваше доказательство.
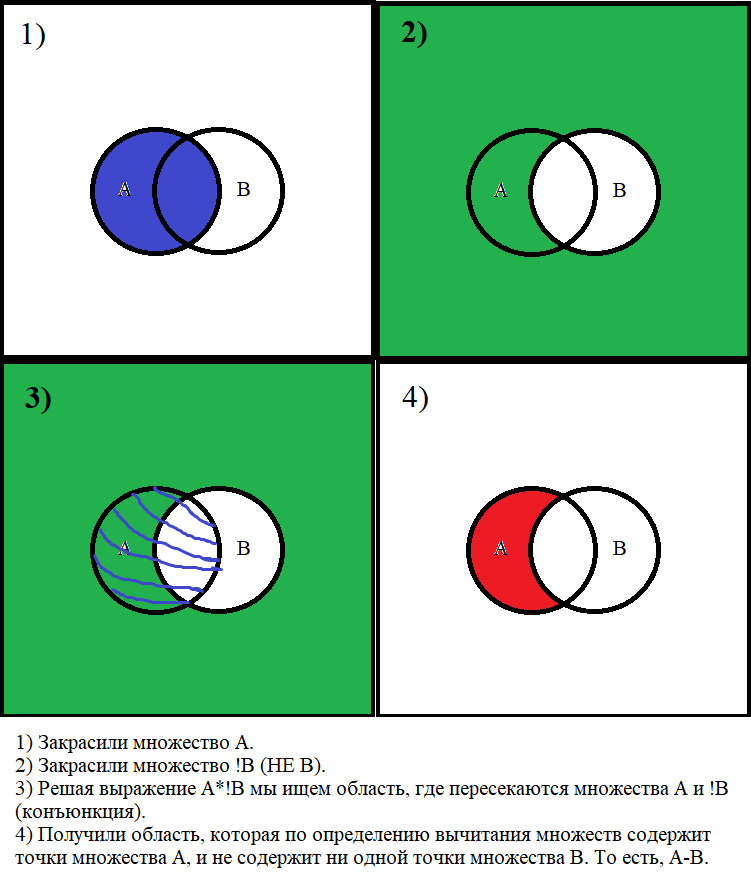
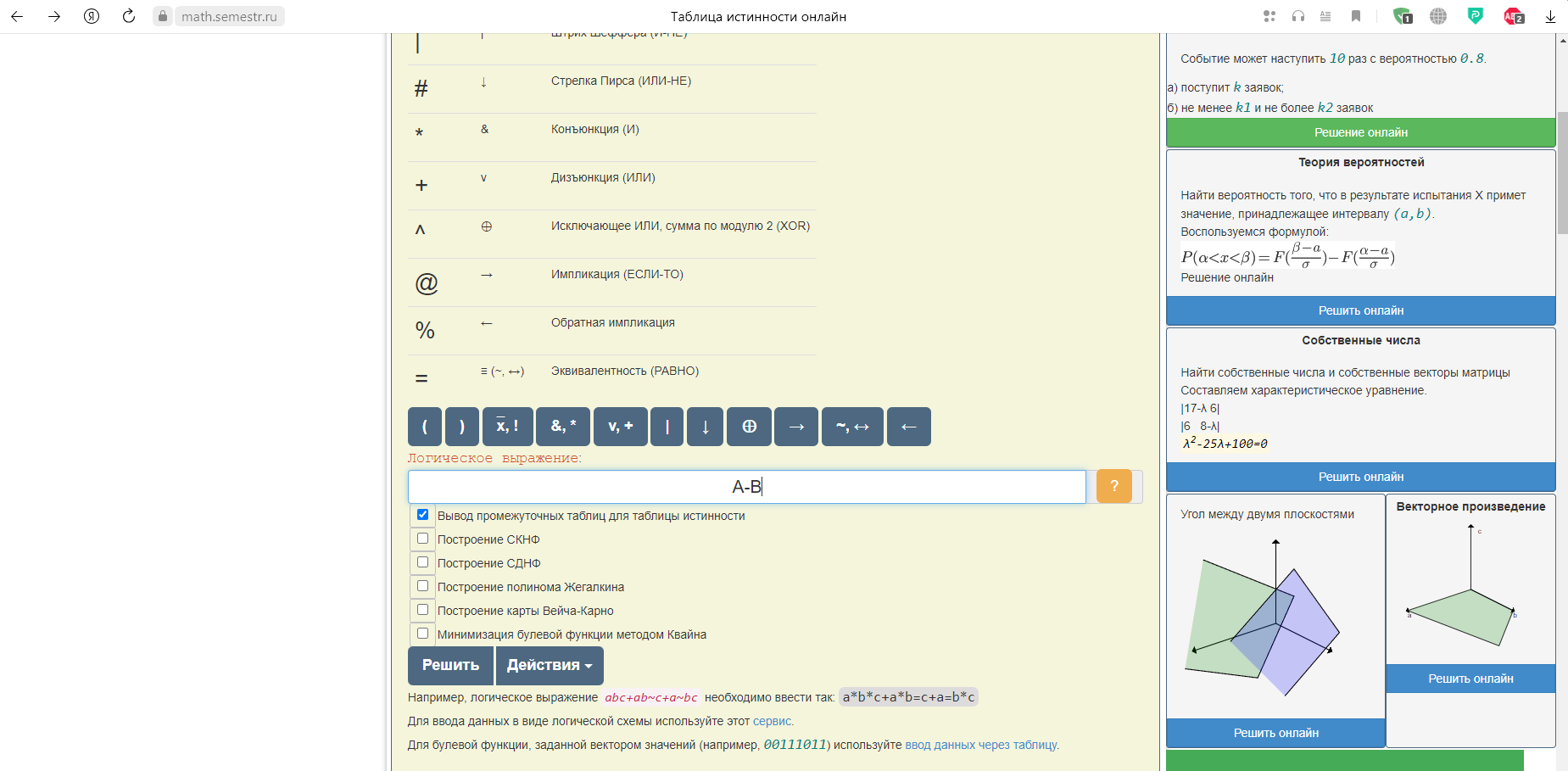
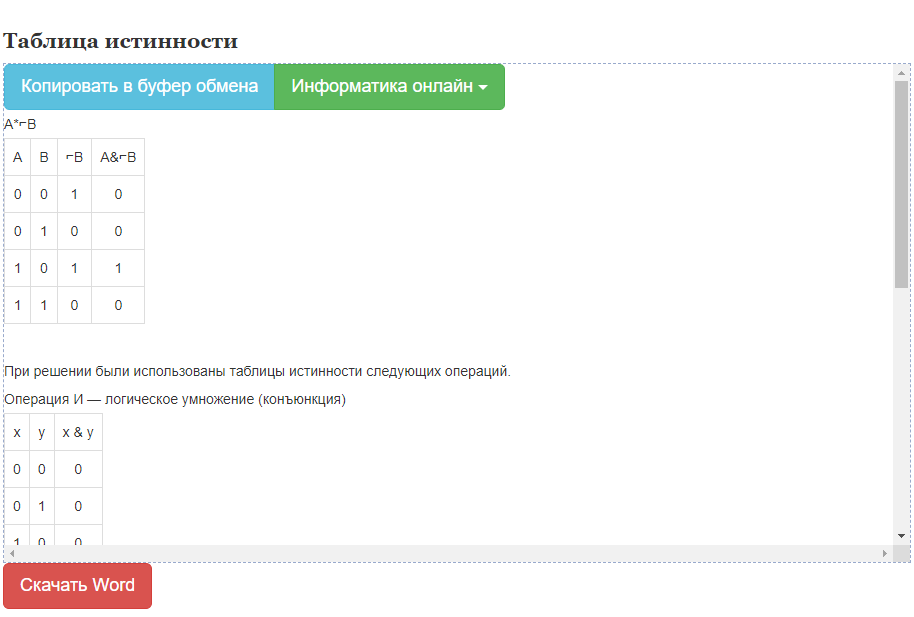
Вот я выше привёл таблицу интстинности вычитания по модулю 2, таблицу xor, они совпали, ч.т.д.
И почему бы тогда не использовать симметричную разность множеств?

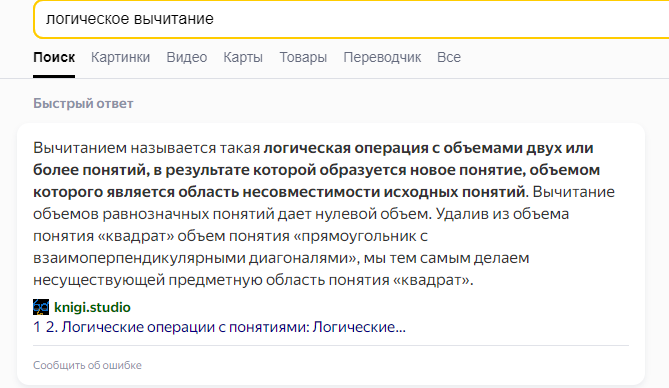
Существует ли логическая операция олицетворяющая вычитание?

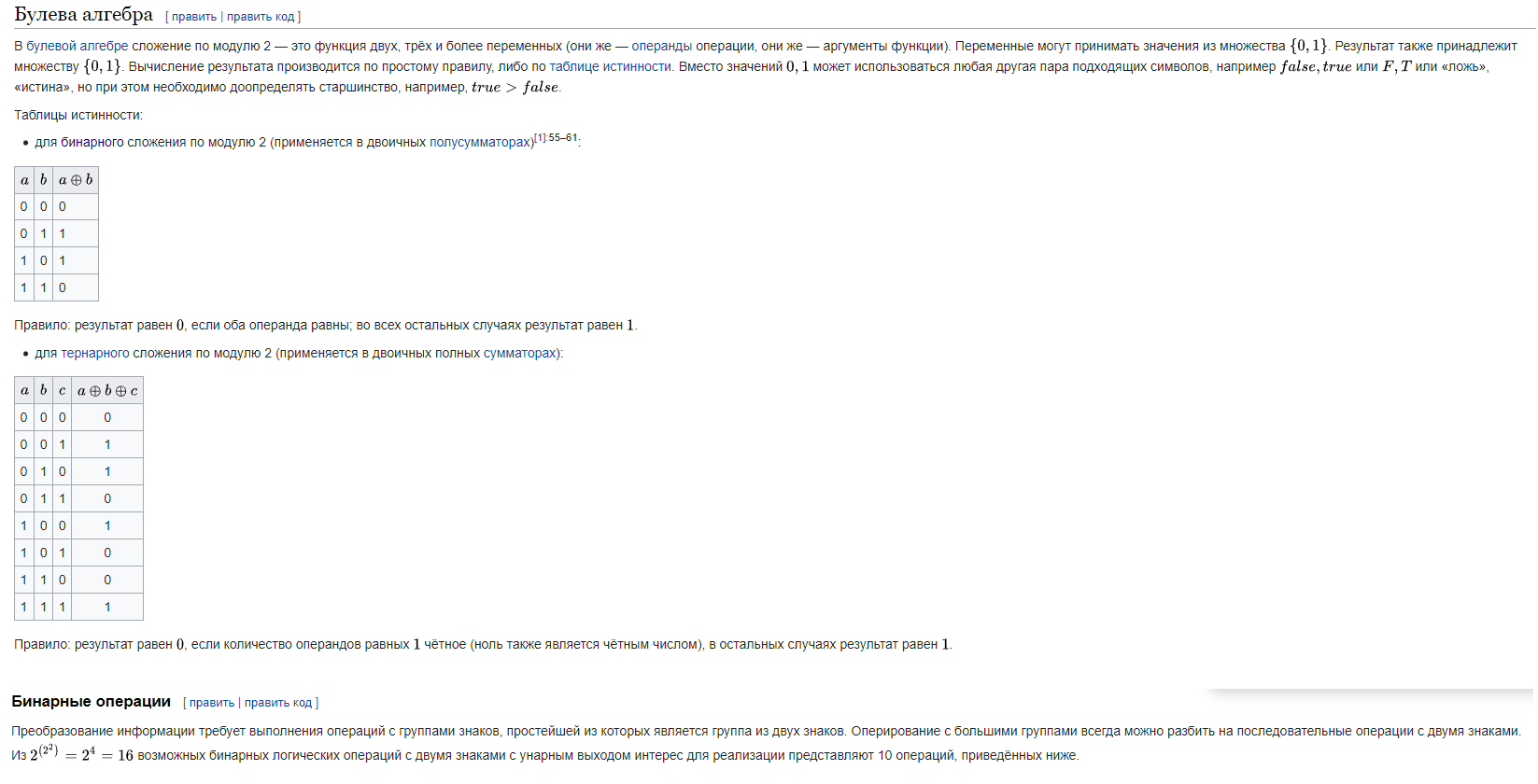
Из одного или нескольких высказываний можно получить другое высказывание, используя логические связки: (конъюнкция, логическое умножение, и), (дизъюнкция, логическое сложение, неисключающее или), ¬ (отрицание, не), → (импликация), ↓(стрелка Пирса), | (штрих Шеффера), (символ Жегалкина, исключающее или, сложение по модулю 2), ~ (эквиваленция), \ (логическое вычитание) и это высказывание называется логической функцией исходных высказываний.
На что я отвечаю, что это xor
Получаем, что A-B=A xor B, следовательно - := XOR.не обманывали товарищей.

ваши ложные выводы не обманывали товарищей

свои тезис-доказательство-вывод
Учитывая, что А - В в булевой алгебре означать может только А·!В, то таблица истинности должна быть следующая:

это не значит, что РАЗЛИЧНЫЕ операции стали одной и той же операцией
mod 2, более того они тождествены. Классическое строгое математическое доказательство.Можно собрать любую нейронную сеть, или длиннющую логическую схему, где из двух входов А и В получится та же таблица истинности
вычитание по модулю происходит в двоичной системе исчисления, а не в булевой бинарной.
Если XOR это вычитание по модулю два, то как быть при наличии трёх и более входов?
Вас спросили, есть ли логическое вычитание, вы сказали, XOR это вычитание по модулю 2
логическая операция олицетворяющая вычитание
остаться проигравшим в явно проигранном споре
Это бинарный оператор или функция от двух аргументов. Никакого третьего аргумента у неё нет.

Берите учебники, ищите определения
Пусть A, B, C — тройка непустых множеств. Бинарной операцией, или бинарной функцией, на паре A, B со значениями в C называется отображение P:A×B→C.

доказательств было предостаточно
аргументы у бинарных операторов не ограничены двумя
никакого отождествления логического и арифметического вычитания не подрузамевается
Сейчас вы использовали софистскую логическую уловку
Для ассоциативной операции результат вычисления x1, x2,..., xn не зависит от порядка вычисления (расстановки скобок)- википедия почти сразу после определения. Черника форте помогает зрению.
Составим таблицу истинности для математического вычитания.
A B A-B
0 0 0
0 1 1
1 0 1
1 1 0
Получаем, что A-B=A xor B, следовательно - := XOR.

википедия почти сразу после определения.
В этом случае нужно использовать правила композиции функций, которые, разумеется, будут отличаться от классических алгебраических (Антикоммутативность, Дистрибутивность и т.п.).
Оператор с функцией...
даже не упомянув что оно по модулю 2
Давайте вам доказательство из теории вероятностей дам
true & false | true с вероятностью 1/16, интересно на это посмотреть. Вы же утвержаете, что сложение и вычитание это эквивалентные операции, только исходя из одинакового результата.
А если в качестве массивов я буду использовать числа А = 7, В = 8, то результат не будет совпадать с таблицей истинности XOR. Почему же, если жто эквивалентные операции?
(7 mod 2) - (8 mod 2) = 1 - 0 = 1, когда true ⊕ false = 1. Убедились? Всё работает как часы. На всё ответил? Удовлетворил?
Ничего не понял, опять формул нет. Какие-то вероятности... Ну давайте, вычислите true & false | true с вероятностью 1/16, интересно на это посмотреть.


Ну давайте проверим вместе: (7 mod 2) - (8 mod 2) = 1 - 0 = 1, когда true ⊕ false = 1. Убедились? Всё работает как часы.

искали только то, что подтверждает вашу "идею", а то что опровергает пропускали, как всегда.
7 - 8 не получилось, попробуйте еще раз.
Повторю вопрос, почему 7 это true, а 8 это false?
Как вам вдолдонить в голову, что это сложение?
Потому что мы работаем на mod 2, где существую только два числа: 0 и 1.

почему 7 это true, а 8 - false?


вычитание в группоиде {0; 1} с циклическим порядком




