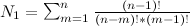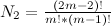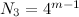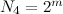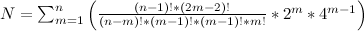Как составить программу «Расставить знаки арифметических операций и скобки чтобы выполнялось равенство»?

Question

[MAXH0]

Где то находил готовое решение, но теперь не могу найти.
Может у кого осталось.

Задача, в принципе, стандартная на перебор. Но лень матушка.

Answer 1

[Mrrl]

Если в формулировке "расставить знаки, чтобы получить 100", то у меня осталось что-то такое:
https://www.dropbox.com/s/vktq0cllod4d34s/LuckyTic...

Answer 2

[Rsa97]

И нехилый такой переборчик получается.
В варианте "расставить знаки и скобки в левой части, чтобы выполнилось равенство":
Пусть строка цифр в левой части имеет длину n.
1. Разбить всеми возможными способами строку на числа. То есть получаем от 1 до n чисел. Количество вариантов разбиения строки из n цифр на m чисел

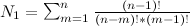
2. Так как в условии сказано про скобки, то операции могут выполняться в разном порядке. Для указания порядка операций по каждому массиву из m чисел можно построить бинарное дерево, используя элементы массива как листья. Каждое дерево будет содержать m-1 вершину. Количество таких деревьев (число Каталана)

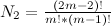
3. Каждая из вершин задаёт одну из четырёх математических операций (+, -, *, /). Таким образом, количество возможных формул для одного дерева

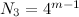
4. Если добавить унарные минусы, то их можно раставить для каждого из m листьев

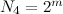
Итого вариантов

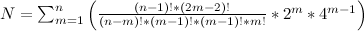
После этого обходом дерева выполняем расчёт и, если результат правильный, выводим дерево в виде выражения со скобками. Вот количество вариантов для разных n (хотя часть из них и окажется дублями или математически неверными из-за деления на 0).

+----+---------------------+---------------------+
|  n | без унарных минусов | с унарными минусами |
+----+---------------------+---------------------+
|  1 |                   1 |                   2 |
|  2 |                   5 |                  18 |
|  3 |                  41 |                 290 |
|  4 |                 320 |               5'938 |
|  5 |               5'073 |             136'770 |
|  6 |              64'469 |           3'379'794 |
|  7 |             859'385 |          87'547'746 |
|  8 |          11'853'949 |       2'345'800'050 |
|  9 |         167'763'361 |      64'477'920'386 |
| 10 |       2'422'342'053 |   1'807'930'569'874 |
+----+---------------------+---------------------+

Мне кажется, или действительно перебор? :-)

Comments

[Mrrl]

Нет, всё несколько лучше. Надо только заметить, что из любой цепочки сложений и вычитаний мы можем убрать все скобки, оставив между знаками операций только мультипликативные термы. Например, a-(b-c) преобразуется в a-b+c. И наоборот - a/(b/c) преобразуется в a/b*c (a,b,c - аддитивные термы). Так что для определения числа комбинаций F(N) для N-значного числа можно рассмотреть все его разбиения на более чем одну группу (их 2^(N-1)-1), для каждого такого разбиения посчитать произведение F(n_i) для элементов этого разбиения, умноженное на 2^(k-1) (k - число групп в разбиении). F(N) будет суммой этих произведений.
Смысл F(N) - число комбинаций, в которых на верхнем уровне стоит операция определённого типа (только мультипликативная или только аддитивная).
Выражение A=B можно записать как A-B=0, то есть для поиска тождеств надо перебрать F(N) комбинаций, аддитивных на верхнем уровне. Некоторые из них будут иметь вид A+B+C+...=0 - им соответствуют тождества с унарным минусом.
Значение F(N) для небольших N:

F(2)=2
F(3)=16
F(4)=130
F(5)=1152
F(6)=10914
F(7)=108368
F(8)=1113186
F(9)=11731584
F(10)=126133186
F(11)=1378070544
F(12)=15255682754

Перебор можно ещё сократить, если разбивать комбинацию на две части примерно равной длины, и брать для каждой из них список значений - а потом их сравнивать.
(В случае 2-2*1*1*2+2=0 "части примерно равной длины" будут иметь длину 1 и 5).

[Rsa97]

Согласен, это гораздо эффективнее полного перебора. Но попробуйте посчитать не просто разбиение массива чисел на группы, а полное количество вариантов выражений, которые можно составить используя n цифр.

[Mrrl]

То, что написано - общее количество выражений со сложением или вычитанием на верхнем уровне. Если считать вообще все выражения, их будет вдвое больше (плюс 1 - на n-значное число), но для поиска тождеств произведения и частные не очень пригодны.
Например, 16 выражений из 123 - это такие:
12+3, 12-3, 1+23, 1-23, 1+2+3, 1+2-3, 1-2+3, 1-2-3,
1*2+3, 1/2+3, 1*2-3, 1/2-3, 1+2*3, 1+2/3, 1-2*3, 1-2/3.
К ним можно добавить "двойственные" (12*3, 12/3,... ,1/(2-3)) и само 123.