Ищу алгоритм анализа нетривиальных данных

Question

[lesobrod]

Контекст вопроса относится к звуку и психоакустике. Но сам вопрос связан с информацией и алгоритмами.

Сначала очень краткое описание контекста. Спектр ноты «нормального» музыкального инструмента состоит из
отдельных линий (гармоник), образующих арифметическую прогрессию по частоте



и спадающих примерно как ~1/f по амплитуде. («Нормальные» — это значит: не колокола, и даже не пан-флейта).
Несколько нот, взятые одновременно (аккорд), образуют «муаровый узор» гармоник:



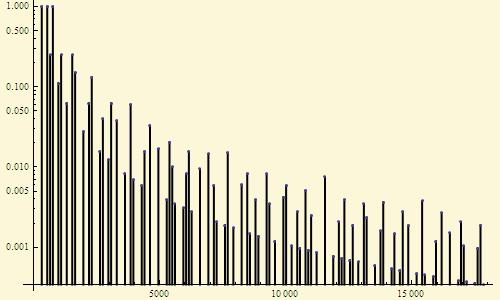
Я разбираюсь с темой консонанса/диссонанса, т.е. степени «приятности» звучания аккорда.
Есть несколько гипотез, как вид спектра влияет на консонанс.

Одна из них гораздо больше связана с информацией и алгоритмами, а не акустикой.
Утверждается, что один из способов, которым слуховая кора ( и тем более фронтальная)
анализирует звук — когнитивный, т.е. спектр воспринимается как целое и мозг подбирает
«алгоритм описания» линейчатого узора.
Если этот алгоритм прост, компактен, то аккорд воспринимается как приятный, созвучный.
Если алгоритм получается «навороченный», то звук оценивается как немузыкальный,
некрасивый. Очевидно, речь идёт о т.н. Колмогоровской сложности.

На уровне описания мне понравилась эта гипотеза. Но хотелось бы получить количественные оценки!
Можно упрощенно сказать, что для любых сложных звуков наш слух инстинктивно пытается подобрать один тон.
Таким образом, можно попытаться оценить, насколько сложный узор аккорда «близок» к ряду гармоник одной ноты.

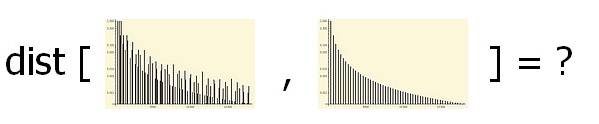
Проблема в том, что опыты показывают — основная частота «виртуальной ноты» может
вообще не принадлежать аккорду!
Вот тут я уже начал тормозить. И вопрос получается такой.
Есть набор данных вида { {f1, a1}, {f2, a2}, .....}, где f — частоты, а — амплитуды.
— Нужен алгоритм оценки, насколько этот набор близок к гармоническому { {f0, a0}, {2*f0, a0/2}, {3*f0, a0/3}, ....} с некоторой (заранее неизвестной) f0.
— Либо, количественная оценка алгоритмической сложности исходного набора

Прошу прощения за некоторую сумбурность, готов уточнить детали.

Comments

[Максим Дьяченко]

Интересная идея.
Не подскажете как вы это сейчас анализируете?
У меня было пару мыслей, хотелось посмотреть на некоторые спектры, и немного с ними поиграться, но я как-то не сообразил как мне увидеть этот самый скользящий спектр и фазу.
преобразование Фурье и вейвлеты помню, но чего-то мне не хватает. Какого-то понимания, чтобы картинка стала на место.
Подскажите с чего начать?

ПЫСЫ: контекст — есть гипотеза, что если заменить звуковой канал визуальным, то при удачном визуальном кодировании глухие смогут не только слышать, но и даже разговаривать. Ведь для глухого проблемы с речью связаны с отсутствием обратной связи — известно, что если человек потерял слух умея разговаривать, то его речь начинает ухудшаться и быстро превращается в непонятную. В общем направление мысли думаю понятное, но с какой стороны к нему подойти, да как создать такие чудо-очки — не понятно. Не понятно даже насколько это реально.

Answer 1

[m08pvv]

Первое что приходит в голову — вэйвлет-разложение с использованием подходящего материнского вэйвлета (например, в виде спектра ноты), после чего просто смотреть на коэффициенты.

Comments

[lesobrod]

Ага, спасибо! Где-то было про то, что алгоритм, подобный вэйвлетам, «встроен» в высшую нервную деятельность.
И в Mathematica 9 тему Wavelet Analysis расширили.

Answer 2

[lesobrod]

Я вот придумал совсем примитивный анализ. У ноты все расстояния между линиями одинаковые,
т.е их (расстояний) дисперсия равна нулю Можно взять все попарные расстояния между линиями в аккорде как набор данных, и посчитать всякие его стат. данные — дисперсию, симметрию и т.д.

Answer 3

[Sayonji]

А причем тут амплитуды? Я ведь верно понимаю, что амплитуды грубо говоря означают громкость? Тогда они практически не влияют на приятность ощущения. Скажем, можно взять обычный до-ми-соль, где до сильно отличается громкостью от ми, которая сильно отличается от соль. Получится вполне нормально звучащий аккорд, однако картинка совсем не будет похожа на первую в топике. А можно наоборот, взять до-до#-ре одинаковой интенсивности, тогда картинка будет ровной.
В общем, кажется роль играют только частоты, интуитивно то же кажется. Ведь, раз там арфиметические прогрессии, всё должно быть достаточно периодично и пофигу на эту гиперболу.
А насчет похожести на равномерность, мне ваша же идея кажется вполне подходящей.
Постройте, говоря простым языком, «зависимость колва полосочек слева от частоты», получится набор точек. А его можно методом наименьших квадратов аппроксимировать прямой (а прямая это как раз равномерное распределение), там уже все дисперсии давно посчитаны.

Comments

[lesobrod]

Да, насчёт частот я определился. Вейвлеты и статистика, а в статистике попробую и наименьшие квадраты.
Думаю, первичное восприятие ближе к статистике, а высших отделах коры что-то вроде вейвлетов.

А вот амплитуды… Это момент очень неоднозначный.
Безусловно, они не играют определяющую роль в консонансе. И вы привели подходящие примеры.
Но вот другой пример. Чтобы его понять надо открыть какой-нибудь простой синтезатор. (Я вообще Synthmaker пользуюсь, там всё из «деталек» собирается). Берём 15-17 синус-гармоник и выставляем их амплитуды.
Случай 1. Все поровну. Поверьте, звук получится неприятный, сразу захочется «убрать высокие».
Случай 2. Пологий спад (необязательно по гиперболе). Весьма музыкально. Можно разные инструменты имитировать, в ранних синтах так и делалось.
Случай 3. Все случайно. Мрак. Для эмо-нойз-психоделики пойдёт, но это не музыкальный звук.

Про аккорды читал, что пианисты интуитивно стараются верхние ноты потише брать.
Предварительный вывод такой — для когнитивной оценки консонанс-диссонанс амплитуды не влияют;
лишь бы слишком не отличались от «нормальных».

В принципе тема раскрыта, всем большое спасибо! Но не буду выбирать «решение». Может, кто еще идей подкинет.
Полную статью на эту тему на Хабре не буду постить — кармы не хватает, и фактически офф-топ.
Но кому интересно, через пару дней можно будет (через профиль) посмотреть материал.

Answer 4

[egorinsk]

> Я разбираюсь с темой консонанса/диссонанса, т.е. степени «приятности» звучания аккорда.

Если я не ошибаюсь, она зависит не от соотношения амплитуд гармоник, а от соотношения частот входящих в него нот.

Вы знаете про соотношение частот нот (имеются в виду основная частота) в созвучных и несозвучных сочетаниях? Этим еще Пифагор занимался. Например, если ноты различаются на 12 полутонов, то это соотношение 2:1, если на 7 пт то 3:2, если на 5 пт то 5:4 (вроде так?). У таких «кратных нот» много совпадающих друг с другом гармоник. Они как бы сливаются при звучании.

Возьмем противоположный пример: ноты, различающиеся на 1пт. У сочетания таких нот, если изобразить спектр, гармоники не совпадают, выглядят сдвоенными палками, находятся близко друг к другу и звучат они не очень-то приятно.

В мажорном аккорде тоже есть какие-то соотношения между частотами звука отдельных нот.

Также, у меня есть ощущение, что мозг умеет объединять гармоники с основной частотой. Например, звуки музыкальных инструментов состоят из гармоник, но мы ведь слышим их как одну ноту, а не несколько. Потому, наверно, амплитуда отдельных гармоник (и характер их изменения во времени) определяет тембр звука, но не «приятность» звучания аккорда.

Comments

[egorinsk]

И еще, мне кажется, вы зря нарисовали график с равномерной осью X. Слух человека хорошо различает частоты в диапазоне речи, а вот высокие частоты не очень.

[egorinsk]

И еще мысль, если вы ищите приятные звуки, наверно стоит начать с анализа звуков музыкальных инструментов, а не примитивных звуков из набора гармоник. Например, в реальных инструментах спектр звука меняется со временем, а отдельные гармоники по амплитуде «дрожат». Если же этого нет, то звук воспринимается как статичный, скучный, электронный, надоедливый.

И если вы этого не учитываете, получается, вы анализируете именно такой, скучный звук.

[lesobrod]

Насчёт амплитуд я уже уточнил. Сильно они, конечно, не влияют; а более тонкие эффекты здесь неуместно рассматривать.

Вообще, уважаемый egorinsk, большое спасибо за такой развёрнутый комментарий,
но это был вопрос не о причинах консонанса/диссонанса,
а о методе анализа данных для описания одной из сторон этого явления (когнитивной).

То, о чём вы упомянули в начале, относится к консонансу/диссонансу по ширине критической полосы, а это совершенно отдельная большая тема.
Хотя, конечно, пифагоровы соотношения работают и в когнитивном случае.

Обе оси должны быть логарифмические, вы совершенно правы. Но, повторюсь, картинки делал для вопроса по алгоритмическому анализу, а не по психоакустике.

А вот о скучности/интересности интервалов и аккордов это просто бездонная тема. На форумклассика.ру её чуть ли не год перетирали. Коротко говоря, вы правы, но всё таки основу консонанса/диссонанса составляет взаимодействие между обертонами.
Не все так считают, но и не я один… гм…
Негармоничность и окраска тембров, разумеется, добавляет в звук свою приятность.
Но если интервал сильно диссонирует (как тритон в равномерной темперации), то его никакими «печеньками» не сделаешь консонансом.

ЗЫ. У меня и так карма маленькая; не уверен, что здесь такие акустические глубины вообще в тему.
Обратите внимание, что я написал в каменте выше.