Нахождение F(x), для которой аргумент (элем. исход) ξ(ω) распределён неравномерно?

Question

[floppa322]

Составил для себя простенький алгоритм для нахождения F(x), если все ω из Ω распределены равномерно:
1. Найти ξ^(-1)(w)
2. Найти l(w) - сумма длин отрезков(ка), которые(ый) ниже горизонтальной прямой ξ^(-1)(w)
3. F(x) = l(w) / L, где L - длина области определения ξ(w)

Пример:
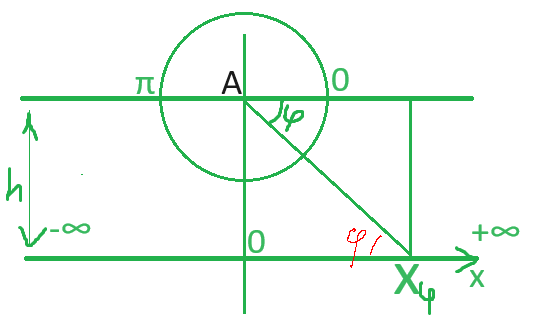
Частицы излучаются из точки A с равномерно распределенным углом φ [0, π] (Ω=[0, π]) и попадают на нижнюю прямую. Найти функцию распределения F(x) координаты падения Xφ


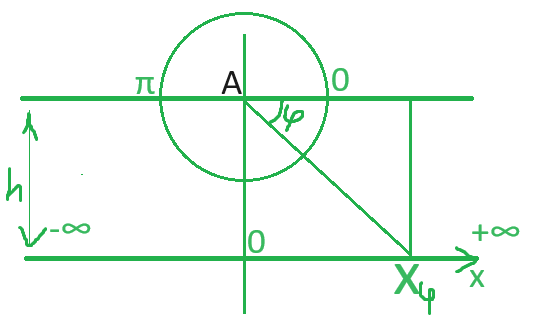
0. ξ(φ) = h / (tg(φ)) = Xφ, φ \ {0, π/2, π}
1. ξ^(-1)(φ) = arctg(h/(ξ(φ))) = φ = arctg(h/x), φ \ {0, π/2, π}
2. l(x) = π - arctg(h/x)
3. F(x) = 1 - arctg(h/x)/π

Вроде бы всё понятно, если φ распределён равномерно, а как изменится алгоритм построения F(x), если φ(или x) распределён неравномерно ? Вроде бы шаги 1-2 останутся прежними, а на 3-й шаг как-то наверное плотность φ должна повлиять?

Answer 1

[Mercury13]

Всё точно так же. Считаем, что φ от −π/2 до π/2!!!!
F_x(u) = p{x < u} = p{h tg φ < u} = p{φ < arctg(u/h)} = F_φ(arctg(u/h))

Соответственно, в твоём случае φ от 0 до π, при непрерывном распределении:
F_x(u) = p{x < u} = p{h ctg φ < u} = [арккотангенс убывает, меняется знак!!] = p{φ > arcctg(u/h)} = 1−F_φ(arcctg(u/h))

Лучше брать arcctg(x/h), чем arctg(h/x) — не нужно делать скидку на то, что мы сидим на двух стульях кусках ОДЗ.

Comments

[floppa322]

Хм, может я что-то не так понял, но я имел в виду, что в исходном решении плотность распределения равномерная - φ∊[0, π] f(φ) = 1/π.
А что делать, если, например, φ∊[0, π] f(φ) = (1/S) * √φ, где 1/S - коэф. нормировки (S площадь под кривой от 0 до π), ну то есть значения π из интервала [0, π] неравномевроятны
Хотя я сейчас сонный, мог что-то не догнать :)

[Mercury13]

floppa322, Для ФУНКЦИИ РАСПРЕДЕЛЕНИЯ — то же самое.
Для ПЛОТНОСТИ — надо множить на коэффициент.

f(u) = F_x(u)′_u = −F_φ(arcctg(u/h))′_u = −F_φ’(arcctg(u/h))·(−1)/(1+(u/h)²)·(1/h) = f_φ(arcctg(u/h))/(h(1+(u/h)²)

[Mercury13]

floppa322, Вроде так.

[Mercury13]

floppa322, А если взять v=u/h, то f_φ(arcctg v)/(h(1+v²))

[floppa322]

Mercury13, хорошо, спасибо, завтра утром подробнее разберусь тогда :)

[Mercury13]

floppa322, В компьютерном деле используется функция распределения (прямая или обратная) всегда, когда её можно эффективно найти. Допустим, для симуляции гауссова распределения проще выкинуть треть сгенерированных чисел и пару (x,y), случайно попавшую в единичный круг, превратить в пару гауссовых, чем считать гадкую функцию. А не попавшую — выкинуть. Но это уже оптимизации. Обычно находят число от 0 до 1, и F^—1(ω).

[floppa322]

Mercury13, ну про обратную функцию от F и случайное число от 0 до 1 я знаю трюк :)

[Mercury13]

floppa322, Полагаю, когда источник случайности дорогой (физический), программисты будут стараться не отбрасывать, а строить аппроксимацию F^—1 получше, через какие-нибудь эрмитовы кубические кривые. Хорошему источнику — хорошая аппроксимация, верно?

[Mercury13]

floppa322, Просто трюк с масштабированием радиус-вектора абсолютно точен, а аппроксимации интеграла ошибок — по определению нет.

Answer 2

[floppa322]

В общем, всё оказалось довольно просто, если φ распределен неравномерно, то алгоритм следующий:

1. Найти ξ^(-1)(φ) (потому что значение исходной кси ξ^(φ) это как раз значение аргумента Fξ(x), чтобы по x находить множества φ (отрезки), которые ниже x
2. Результирующая Fξ(x) должна для каждого отрезка (которые ниже x) [a,b] просто вычислить вероятность множества этих [a, b] и суммировать их, используя Fφ(x): Fφ(b) - Fφ(a) (сами a и b это значения ξ^(-1)(φ))

Способ, описанный вопросе, это просто частный случай для равномерного распределения :)