Как найти минимальное число прохождений по автомату до конечного состояния с N вероятностью?

Question

[SergeySerge11]

Не могу понять как решить задачу.
Есть граф, допустим такой
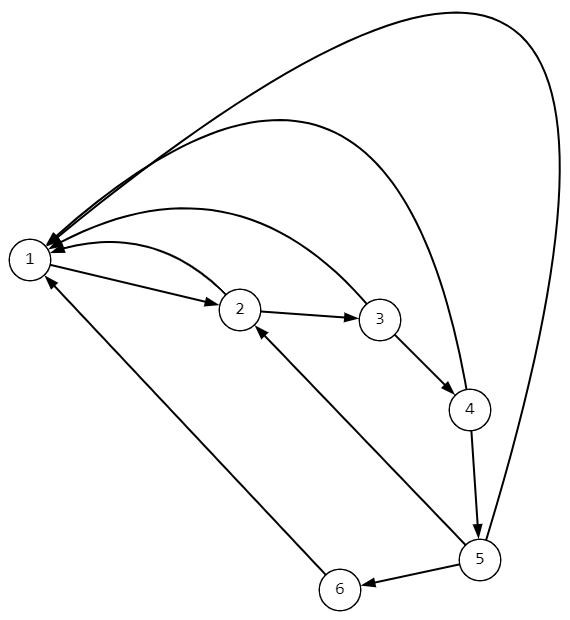
Задача, оценить минимальное число итераций прохождений по состояниям до состояния 6. С 99% вероятностью?
То есть сколько раз потребуется изменить состояние что бы гарантировано с 99% вероятностью его пройти.
Из схемы видно что в состоянии 1 система будет чаще чем в 2, 2 чаще чем в 3, ... а в 6 будет допустим раз в 50 итераций попадать с 99% вероятностью(из симуляции цифра).
Не могу понять, это связано с цепью маркова, или немного другая задача, ведь по моему условию, я не знаю, вероятностей переходов, но возможно их надо вывести симуляциями(хотя там по равной доли вероятности с любого N состояния в другое соседнее можно попасть).
К примеру матрица вероятности переходов будет такой
0.5 0.5
0.33 0.33 0.33
0.25 0.25 0.25 0.25
.... не знаю, дает ли что-то.
И можно ли вывести уравнение для различных графов.

Comments

[Wataru]

Нн совсем ясно условие. Надо найти такое минимальное K, что путь из K переходов по цепи посетит заданную вершину хотя бы раз с вероятностью не меньше p? Или надо за K шагов оказаться в вершине?

А без вероятностей переходов, вообще говоря, задача не имеет смысла. Возможно там действительно равновероятные переходы. Уточняйте условие оттуда, где его взяли.

[mayton2019]

Это точно не условие из учебника. Как-то сбивчиво написано и неоднозначно.
По виду похоже на Марковские сети. Есть ли там формула достижимости
узла за N шагов - не знаю. Надо просто открыть учебник и читать.

Проще такую задачу решать симуляцией. Типа генетического отбора.
Генерируем случайные матрицы вероятностей переходов, симулируем
процесс и меряем фитнесс.

Answer 1

[Wataru]

Есть простой трюк сильно упростить задачу: Измените переходы из "конечной" вершины - она теперь с вероятностью 100% будет вести только в саму себя. Таким образом, процесс хотя бы раз достигший вершины, навсегда в ней останется.

А вопрос из задачи (если его понимать как: минимальное количество шагов, чтобы хотя бы раз посетить конечную вершину с вероятностью >99%) становится эквивалентен: минимальное количество шагов, чтобы быть в конечной вершине с вероятностью не меньше 99%.

А тут уже надо найти минимальное число k, такое что соответствующее значение в матрице A^k было бы > 0.99. A тут - это матрица переходов.

Можно или в тупую умножать матрицу саму на себя, пока значение в строке начальной вершины и столбце конечной вершины не станет достаточно большим. Это будет O(N^3*ответ). Или можно делать хитро: бинарным поиском перебирайте степень, а внутри логарифмическим возведением в степень считайте A^k. Это будет O(N^3*log(ответ)^2).

Answer 2

[Александр Скуснов]

Вроде, марковский процесс описывает конечные (предельные) значения вероятностей при любых начальных условиях.