Как правильно найти и описать аппроксимацию данных нормальным распределением со смещенным центром?

Question

[Даниил Бакалин]

Суть вопроса. Есть данные о вероятности встретить некоторый вид в зависимости от высоты над уровнем моря:

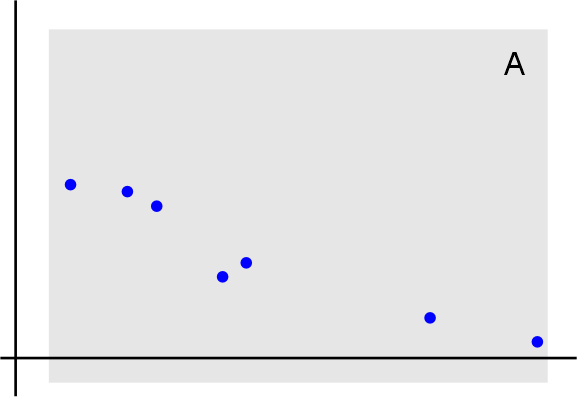
Серым фоном показан диапазон высот где в принципе проводились поиски, т.е. он ограничен.

Нужно найти точку максимальной распространенности вида (т.е. на какой высоте его больше всего).

Так как распределение нормальное, то по сути нужно найти центр этого нормального распределения.
Стандартные функции определения нормального распределения по выборке, предполагают, что оно равно мат. ожиданию выборки. Т.е. как-то так:


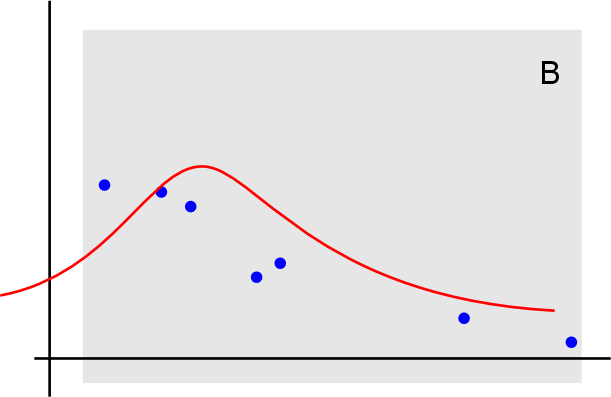
Но это не учитывает, что центр может быть за пределами анализируемого диапазона. И в данном случае, данные гораздо лучше аппроксимируются как-то так:


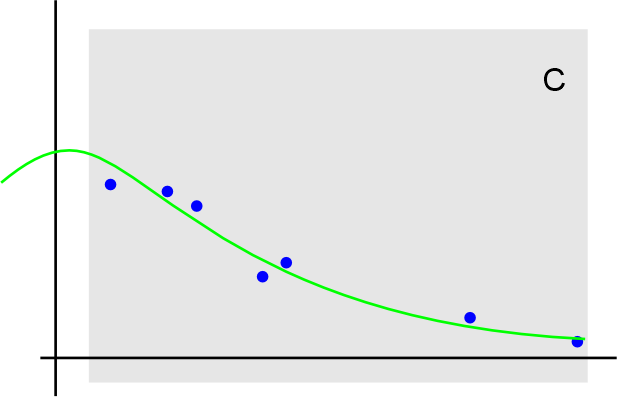
Для нахождения параметров такого распределения я написал небольшой скрипт на питоне который тупым перебором параметров нашел нужные распределения. И результат неплох, в смысле соответствует представлениям о реальном характере произрастания растений. Но возникло два вопроса:

1. Как на деле определяются параметры такого смещенного нормального распределения? Может есть стандартные функции/алгоритмы для аналитического решения задачи?

2. (и главное) Как это все описать правильным с т.з. мат. статистики языком? Мне нужно изложить весь алгоритм в статье, а я довольно далек от мат. статистки, и боюсь переврать термины. Можете подкинуть какие-то правильные формулировки, для этого случая?

Понимаю, что совет "возьмите учебник такой-то и за полгодика освойте основы" - классный и очень приятный советующему. Но надеюсь на помощь людей живущих в реальном мире и понимающих, что возможности не всегда совпадают с желаниями.

В любом случае, спасибо, за любые советы!

Answer 1

[Максим Припадчев]

И так о сути вашей задачи. Перед вами "случайная выборка" sample distribution. Вы утверждаете что общее распределение (population distribution) нормально. Откуда вы это взяли я не знаю, но допустим может условие проблемы таково. Функция нормального распределения имеет два параметра среднее (mean) и стандартное отклонение (standard deviation). Общий вид N(mu, std). Ваша статистическая задача это осуществить аппроксимацию этих параметров на основе данных случайной выборки (sample).

Нужно найти точку максимальной распространенности вида (т.е. на какой высоте его больше всего).

У непрерывных распределений не бывает точек, бывает интервалы. Вероятность в любой точке равна нулю, это одно из главных различий дискретного pmf (probability mass function) от непрерывного pdf (probability density function).

Стандартные функции определения нормального распределения по выборке, предполагают, что оно равно мат. ожиданию выборки.

Что это вообще значит, математическое ожидание это параметр функции распределения, что значит равна вообще ничего не понял.

Но это не учитывает, что центр может быть за пределами анализируемого диапазона

Вообще ничего не понял, есть распределение что такое предел анализируемого диапазона где вы это нашли?

Теперь к ответу на оба ваши вопроса:
На ваших графиках попытка аппроксимировать pdf, для данных на основе наблюдений. В реальности это делается ну например методами MLE (Maximum Likelihood Estimation) Это числовой метод. В том числе полно примеров и на python. Так и гуглить python maximum likelihood estimation normal distribution. Аналитические методы тоже есть конечно. гуглить population mean from sample distribution. Ну и там в определенном интервале будет лежать mean. Но аналитические методы подразумевают слабовыполнимые допущения нужно знать стандартное отклонение популяции например, по этому на практике использует числовые то есть MLE. По терминалогии это классическая статистическая задача на основе выборки осуществить (statistical inference) то есть аппроксимировать параметры population distribution. Точную терминологию (на русском) смотри, в вики. Я привык все это дело на английском делать.

Comments

[Даниил Бакалин]

Спасибо за ответ! Стало понятнее куда копать. То что на английском - отлично, я на нем и пишу статью.

На счет диапазона - поясню. Смысл в том, что есть область где в принципе искали вид. В этой области высоты над уровнем моря ограничены (от 300 до 1000 м.). Было сделано множество находок вида, в разных точках (а в некоторых точках искали, но не нашли).

После чего я разбил весь диапазон (300-1000 м), на 14 ступеней (по 50 м. каждая), и вычислил вероятность найти на этой ступени вид (как отношение числа находок вида, к числу точек поиска). По итогу получил график, примерно как на картинке A.

Если попробовать найти нормальное распределение для этих данных (например в excel), то его центр всегда будет где-то внутри того диапазона высот где проводились поиски. (рисунок B), но это не всегда так. Может быть ситуация когда центр распределения вида находится ниже 300 или выше 1000 м. (этот вариант показана на рисунке C).

Судя по вашему ответу, я так понимаю, что действовал в целом правильно, но я не знал, что есть такие методы как MLE и поэтому костылил велосипед. Попробую тему изучить и применить. Так что спасибо еще раз.

Если с учетом моих пояснений вы сможете дать еще какие-то советы/уточнения - буду очень признателен.

Спасибо)

[Максим Припадчев]

Даниил Бакалин, Я слегка дополнил ответ парой предложений относительно аналитических методов. Хотя все они используются только в обучении (в институтах), на практике MLE (это не один алгоритм, а класс алгоритмов). Числовой метод, для нахождения наиболее вероятного параметра случайной переменной на основе наблюдаемых данных. Ты должен знать что такое случайная переменная. X - наблюдаемые данные. распределение пусть N - нормальное. MLE(X,N) - вернет. Наиболее вероятные парметры функции N(mu, std) которые "произвели данные X".

Не надо диапазонов. Надо занимать инферентивной статистикой. Есть данные X - наблюдения. Мы говорим есть нормальная случайная перменная которая произвела эти данные у этой случайной переменной есть парметры N(mu, std). Так вот используем MLE для того что бы апроксимировать эти параметры. Когда наша модель готова, то мы можем задавать вопросы какая вероятность чего то там больше меньше в интервале. Нам надо создать МОДЕЛЬ. раз ты говоришь распределение популяции нормальное МЫ знаем формулу модели загугли normal pdf и ты получишь большую формулу с двумя параметрами и одной перемнной. параметры это mean и std. Вот их нам и надо аппроксимировать. Есть они значит есть модель. Дальше любой вопрос о верояности какого то события это пару строчек кода c использованием scipy и sympy. Вот для понимания

mu = 2
std = 1
from scipy.stats import norm
X = norm(mu,std)
result = X.rvs(5)
print(result)

Мы будем иметь массив из 5 РЕАЛИЗАЦИЙ нормального распределения из случайной переменной X с mean=2, std=1. Так вот твоя задача ОБРАТНАЯ, ты не знаешь чему равен mean а чему std. Но зато у тебя есть массив реализций result. И MLE аппроксимирует mean и std или только mean если нужно.

[Даниил Бакалин]

Максим Припадчев, я разбил высоты на диапазоны, так как не очень представляю как иначе получить случайную переменную.

Смысл такой. У меня изначально есть список, условно 100 точек где проводился поиск вида. По каждой точке у меня известно на какой высоте над уровнем моря она находится, а также известно был в этой точке найден вид или нет.

При этом точки сбора по высотам распределены неравномерно. На какой-то интервале высот может быть много точек, на каком-то - мало.

Так как я не очень представляю какими методами такие данные (в "сыром" виде) можно анализировать, то я просто разбил весь диапазон высот на интервалы по 50 м. И по каждому посчитал сколько точек в интервал попало, и в скольких точках из тех что попали в интервал - вид был найден.

Так как вероятность произрастания вида в конкретной точке связана с большим числом случайных параметров, согласно ЦПТ, обычно считается, что распределение вида по высоте нормальное. Соответственно и мое отношение числа находок вида в некотором интервале высот, к общему числу точек где этот вид искали - тоже должно иметь нормальный характер распределения.

Ну а дальше вроде все понятно. Кроме того как это все описать, правильным языком)) Но с этим буду разбираться.

[Максим Припадчев]

Даниил Бакалин, В корне не то, ты применил дискретизацию сначала, твое распределение дискретно, а потом говоришь оно нормально, нормальное распределение это непрерывная случайная переменная, а с твоих слов у тебя дискретная.

я разбил высоты на диапазоны, так как не очень представляю как иначе получить случайную переменную.

ОТВЕТ MLE. либо работай с дискретной переменной либо с нормальной, но не смешевай одно с другим это полная глупость.

В принципе раз это не условие что распределение нормальное, а согласно ЦПТ что теория, на практике мы от без выходности часто говорим допустим данные распределены нормально, то можно применять nonparametric methods KDE (kernel density estimation). https://www.statsmodels.org/dev/examples/notebooks..., nonparametric это класс методов, когда мы не делаем допущение о форме population distribution. Вообще открывай если используешь python statsmodels, что MLE что KDE что дискретные модели. Это все там.

Вообще, я надеюсь что ошибаюсь, но ты точно хорошо понимаешь что такое случайная переменная? Почитай в вики. Я не буду объяснять возьму практику. Например мы кидаем кубик на случайная переменная будет равномерно распределенной и иметь вид U(1,6). Что означает U-uniform, с одинакавой вероятностью выбираем число от 1 до 6 включительно. РЕАЛИЗАЦИЕЙ такой случайной переменной будет число от одного до 6. зачем нам эта переменная затем что у ней много математических свойств. И мы имея эту переменную может считать вероятности. Инферинтивная статистика в том числе занимается методами нахождения параметров для таких переменных, или например функции распределения для неизвестной переменной. В данном случае если бы наши данные были бы много результатов броска кубика мы бы нашли что это равнораспределенная дискретная случайная переменная на интервале (1,6).

Так вот твоя задача создать такую переменную (естественно не равнораспределенную а как ты утверждаешь нормальную или какую то другую кастомную). И потом когда она у тебя есть, считать в рамках нее вероятности. А не считать вероятности на сырых данных это глупость. Потому что ты говоришь у меня в каком то интервале точек больше значит там вероятность больше. Вероятность определяется по формуле для каждой случайной переменной она своя. Без модели распределения НЕТ НИКАКИХ ВЕРОЯТНОСТЕЙ.

Вообщем как то так. Все я больше чем надо уделил внимания этому вопросу.

[Даниил Бакалин]

Максим Припадчев,

Потому что ты говоришь у меня в каком то интервале точек больше значит там вероятность больше

Не так. Я говорю не о числе находок, а об отношении.
В диапазоне от 500 до 550 метров, было проанализировано 25 локаций. Из них в 8 локациях вид был найден. Значит вероятность встретить вид на этом диапазоне высот (в рамках данного исследования) 8/25 = 32%.

Спасибо за подсказку насчет дискретности. По сути нет ничего проще применить оконную функцию. и определить непрерывную переменную как такое же отношение, но на диапазоне (X-25, X+25).

В любом случае спасибо за ответы.

[Максим Припадчев]

Даниил Бакалин, В диапазоне от 500 до 550 метров, было проанализировано 25 локаций. Из них в 8 локациях вид был найден. Значит вероятность встретить вид на этом диапазоне высот (в рамках данного исследования) 8/25 = 32%. Нет и еще раз нет. Ты говорил распределение нормальное - а это условие для равномерно распределенного.

На диапазоне от 500 до 550 метров, существует одинаковая вероятность встретить вид. Задача должна звучать вот так. Тогда это не нормальное распределение (normal distribution), а равно распределенное (uniform distribution).

25 локаций конечно маловато для статистических выводов. И формула будет не совсем 8/25, добавится поправка что это sample distribution. Но логика твоя - что твое распределение uniform а не normal.

Ну да ладно дело твое.

[Даниил Бакалин]

Максим Припадчев, Да нет же.
Я писал выше, у меня весь диапазон 300 - 1000 м.
Я разбил его на куски по 50 м,
Фрагмент 500 - 550 - это просто один кусок. Для примера.

Всего локаций где искали вид больше 1000.
Просто на (500-550) выпало 25 локаций. Из них в 8 вид был найден.
Какое распределение внутри фрагмента 500-550 - мне не важно. Мне важно какое распределение на всем диапазоне 300 - 1000.

У меня получается, например
300-350 ---- 2 локации, 0 находок
350-400 ---- 5 локаций, 1 находка
400-450 ---- 12 локаций, 4 находки
450-500 ---- 8 локации, 5 находок
и так далее...

Но я уже понял, что в данном случае величина будет дискретной. Применять нормальное распределение нельзя. Поэтому я возьму оконную функцию, и смогу для любого X от 300 до 1000 - сказать, что в окрестностях X (от X-25, до X+25) - у меня M(x) локаций, и N(x) - находок.
И непрерывная случайная величина p(X) = N(x)/M(x)

Если потом такую функцию нормировать - должна получиться нормальная плотность вероятности (не уверен что терминологически правильно написал). Я статистику изучал много лет назад.