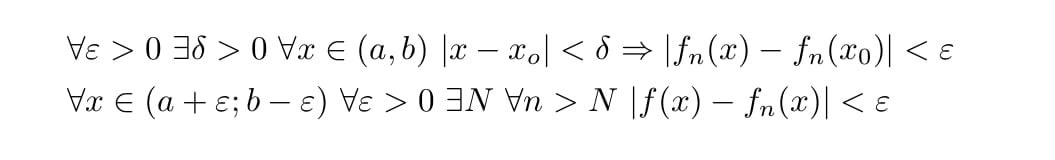Доказательство простого факта. Математический анализ, равномерная непрерывность. Как?

Question

[sresort]

Дано: последовательность функций fn, они непрерывны на (a,b) и ряд сходится равномерно (а+з,b-з) . Нужно доказать что итоговая функция будет непрерывной на всем интервале от (a;b)
Подскажите, пожалуйста как подступиться

ну вот по идее что нам дано

просто воспользоваться теоремой о непрерывной сумме функционального ряда не получается,т.к у нас равномерная сходимость немного меньше(внутри (a,b), не покрывает полностью (a,b)

Comments

[Griboks]

А почему область сходимости задается через з? Мне кажется, в определении равномерной сходимости ее нет. Это доп. условие задачи?

[sresort]

Griboks, Это такое эпсилон :)

[hint000]

sresort, записано как-то не по-русски не по-математически. "Для любого эпсилон" уже после того, как этот эпсилон встретился в формуле - это как вообще? Бессмыслица, IMHO.

[sresort]

hint000, согласен, немно некорректно, просто я тем самым хотел подчеркнуть что epsilon одинаковый
так как речь идет о равномерной непрерывности

[hint000]

sresort,

хотел подчеркнуть что epsilon одинаковый

Если справа и слева epsilon одинаковый, тем более становится непонятно, что такое вообще (a+epsilon, b-epsilon). "Для любого epsilon, большего нуля" значит, что можно взять в частности epsilon=b-a>0, тогда (a+epsilon, b-epsilon)=(b, a).
Я лишь хочу сказать, что в условиях какая-то неточность или недосказанность.

Answer 1

[Wataru]

Я так понял в условии на самом деле говрится, что для любого достаточно маленького z (0 < z < Z0) функциональный ряд равномерно сходится на (a+z, b-z)

Все-равно можно взять теорему о непрерывности предела равномерно сходящегося ряда непрерывных функций, только надо чуть-чуть пошевелиться дополнительно.

Пусть есть a<x0<b. Возьмем z = min(Z0, (x0-a)/2, (b-x0)/2). Используем данное, что ряд равномерно сходится на отрезке (a+z,b-z), а значит F на этом отрезке непрерывна. Значит F непрерывна в точке x0 (ведь мы так z подобрали, чтобы x0 в этом интервале лежала). Мы взяли любую точку x0 из (a,b), а значит F непрерывна на всем интервале.

Edit: Если же в условии тупо дана равномерная сохдимость на каком-то интервале (c,d) (a < c < d < b), а не для сколь угодно близкого к (a,b) вложенного интервала, то, очевидно, что непрерывности там никакой и нет.