Полный перебор можно существенно сократить не перебирая конкретные перестановки цифр: если выбраны цифры d
i, i = 1...m, среди которых есть группы одинаковых, с количеством цифр в каждой из этих групп c
j, j = 1...k, то из этих цифр можно составить
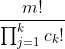
разных чисел. Это число не зависит от конкретно выбранных цифр, только от размера групп одинаковых цифр, т.е. его значение можно посчитать раз и закешировать. Остаётся перебрать все выборки по m цифр из исходных n, их
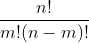
, и для каждой из них, подсчитав размеры групп одинаковых цифр, определить, сколько можно составить разных чисел.