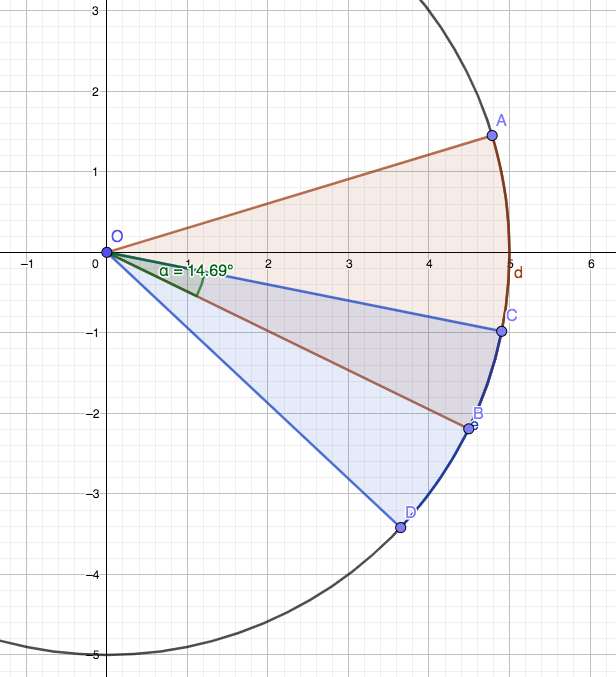
Одно из решений. Пусть сектор A описывается упорядоченной парой {A1,A2}, т.е. сектором считается область получающаяся при обходе окружности по часовой стрелке от точки А1 до точки А2.
1. Привести значения всех углов к диапазону от [0, 2pi).
2. Если A1 > A2, то разобъём сектор на два: S1 = [A1, 2pi) U [0, A2].
3. С помощью алгебры множеств и алгоритма пересечения обычных отрезков можно найти пересечение:
[A1, A2] ∩ [B1, B2] - обычный алгоритм
( [A1, 2pi) U [0, A2] ) ∩ [B1, B2] = ( [B1, B2] ∩ [A1, 2pi) ) U ( [B1, B2] ∩ [0, A2] ) - для каждого из пересечений обычный алгоритм
( [A1, 2pi) U [0, A2] ) ∩ ( [B1, 2pi) U [0, B2] ) - очевидно, что пересекаются как минимум в точке 0