Привет. Меня зовут Petyr.
Код написан в среде WX Maxima.
Есть система нелинейных уравнений :
f_1(x,y)=sin(x + y) − 1,1x + 0, 2 = 0;
f_2(x,y)=x^2 + y^2 - 1=0;
Из графика ниже видно, что данная система имеет четыре корня
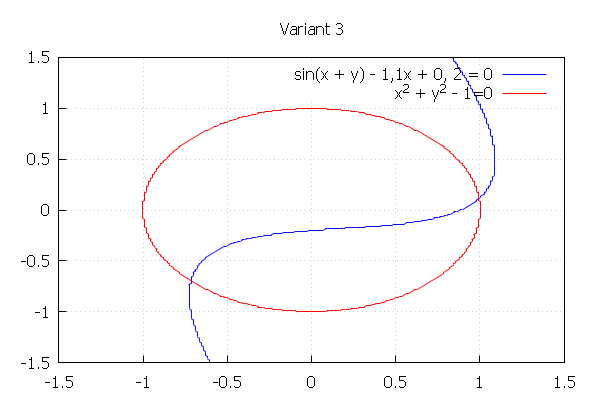
В качестве начального приближения можно взять x1 = 1, y1 = 0.5 и x2 = 1, y2 = -1
Попробуем решить нашу систему относительно x и y:
x = (sin(x+y)-0.1*x+0.2);
y = sqrt(1-x^2);
Зададим соответствующие функции:
g1(x,y):= (sin(x+y)-0.1*x+0.2);
g2(x,y):=sqrt(1-x^2);
Зададим точность и начальное приближение:
x:1; y:0.5; epsilon:10^(−5); n:0;
Запускаем цикл, условие прекращения цикла: расстояние между двумя последовательными
приближениями меньше эпсилон.
unless (float(g1(x,y))−x)^2+(float(g2(x,y))−y)^2<epsilon^2 do
(x0:float(g1(x,y)),y0:float(g2(x,y)),x:x0,y:y0,n:n+1);
Но в итоге maxima считает очень долго и так и не дает ответ. Может проблема в сходимости функций?
Cходимость гарантируется, когда
L0 * f(штрих)(x)>0, где
L0=1/f(штрих)(x0)
L(f1)=-1.657908226985588*del(-0.5) (del - дифференциал)
L(f2)=0.6666666666666669*del(-0.5)
Любая помощь и подсказка будет оценена.
