Как изменить фильтр Калмана, чтобы результат был похож на огибающую исходного сигнала в Matlab?

Question

[tj57]

Взял реализацию фильтра Калмана из этих статей: https://clck.ru/FSbT2, https://habr.com/ru/post/166693/
В моей задаче в условии дан сигнал, который выглядит следующим образом:

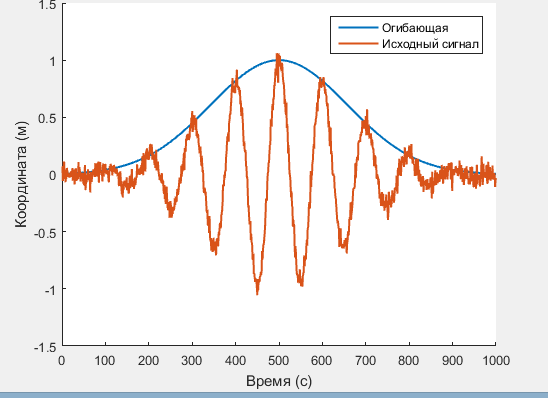
for x = 1:N
    A(x) = exp((-(x-500)^2)/50000);
    y(x) = A(x)*cos(2*3.14*0.01*x)+normrnd(0,sigmaPsi);
end

После применения фильтра Калмана получился результат, практически повторяющий исходный сигнал (как в задаче из вышеуказанных источников):

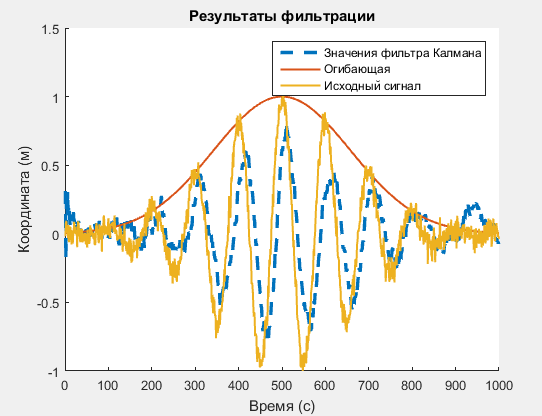
Мне же нужно, чтобы график фильтра Калмана был наиболее близок не к исходному сигналу, а к его огибающей. Соответственно, нужно немного поменять сам алгоритм фильтра Калмана:

for t=1:(N-1)
    eOpt(t+1)=sqrt((sigmaEtaFilter^2)*(eOpt(t)^2+sigmaPsi^2)/(sigmaEtaFilter^2+eOpt(t)^2+sigmaPsi^2)); %минимизация значения ошибки
    msum = msum + eOpt(t+1);
    sum = sum + (eOpt(1))^2;
    K(t+1)=(eOpt(t+1))^2/sigmaEtaFilter^2; %выражение для ошибки
    xOpt(t+1)=(xOpt(t))*(1-K(t+1))+K(t+1)*z(t+1);
end;

Как это можно сделать ? Долго пытаюсь разобраться, но пока безрезультатно.
Код программы :

N = 1000;
sigmaPsi=0.05; %реальные погрешности (ошибка модели)
sigmaEtaModel=0.5; %ошибка измерений прибора
sigmaEtaFilter = 0.8;
k=1:N;
x=k;
for x = 1:N
    A(x) = exp((-(x-500)^2)/50000);
    y(x) = A(x)*cos(2*3.14*0.01*x)+normrnd(0,sigmaPsi);
    z(x)=y(x)+normrnd(0,sigmaEtaModel); 
end
%kalman filter 
xOpt(1)=z(1); %хорошее приближение для истинной координаты
eOpt(1)=sigmaEtaFilter; %дисперсия
msum = eOpt(1); 
sum = (eOpt(1))^2; 
for t=1:(N-1)
    eOpt(t+1)=sqrt((sigmaEtaFilter^2)*(eOpt(t)^2+sigmaPsi^2)/(sigmaEtaFilter^2+eOpt(t)^2+sigmaPsi^2)); %минимизация значения ошибки
    msum = msum + eOpt(t+1);
    sum = sum + (eOpt(1))^2;
    K(t+1)=(eOpt(t+1))^2/sigmaEtaFilter^2; %выражение для ошибки
    xOpt(t+1)=(xOpt(t))*(1-K(t+1))+K(t+1)*z(t+1);
end;
sr = msum/N;
vdisp = sum/N - sr^2; 


hold all;
plot(k,xOpt,'--','linewidth',2.5);
plot(k,A,'linewidth',1.5);
plot(k,y,'LineWidth',1.5); 
title('Результаты фильтрации'); 
xlabel('Время (с)');
ylabel('Координата (м)'); 
legend('Значения фильтра Калмана', 'Огибающая','Исходный сигнал');

Answer 1

[d'Ivan]

По-моему, с помощью фильтра Калмана можно только сглаживать исходный сигнал, но не получить "огибающий".
Сигнал похож на амплитудную модуляцию (радиосигнал).

https://en.wikipedia.org/wiki/Envelope_detector
https://www.mathworks.com/help/dsp/examples/envelo...

Comments

[tj57]

Нет, вопрос в том, как мне изменить алгоритм фильтра таким образом, чтобы его график был близок к огибающей. Сама огибающая построена так:

for x = 1:N
    A(x) = exp((-(x-500)^2)/50000);
end