Как найти оптимальный путь для каждой пары элементов так, чтобы пути соединительных линий не пересекались?

Question

[havemanyquestions]

Здравствуйте.
Имеется такой рисунок. Задавая пары: 1-5, 2-9 и т.д, необходимо их соединять линиями. Точки для возможных линий и соединений - квадрат, составленный из NxN элементов, где N - количество соединяемых элементов одной из соединяемых групп с макс. кол-вом элементов. Нужно соединять линии так, чтобы каждая пара была соединена с другой, и не возникало тупиковых ситуаций, как с красными линиями. При этом линии могут проходить или вертикально, или горизонтально, никаких диагоналей.



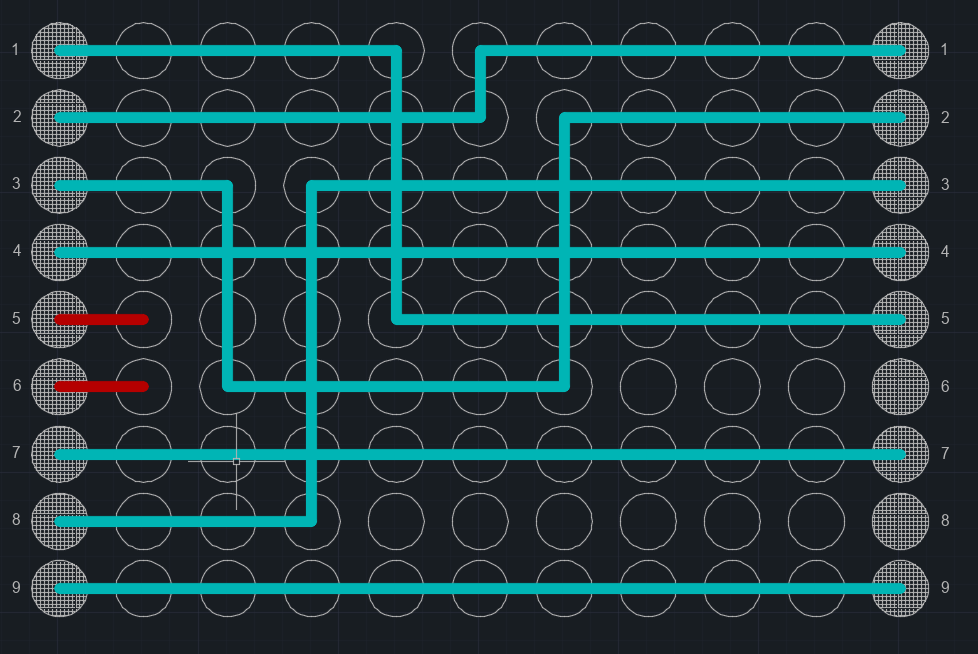
К какой области знания относится рисование, алгоритм данного рисования, вычисление этого самого оптимального пути для каждой пары точек? Что это за алгоритмы, можно простые примеры для, например, двух групп элементов по 3 с каждой стороны?

Укажите хотя бы, в какую сторону смотреть?

P.S. И, как меня верно поправили, есть еще одно условие, забыл указать, линии не должны накладываться, но пересекаться могут.
P.P.S. Поправка. Решений нет при указанном условии. Добавляем еще одно условие - линии могут пересекаться по диагонали.

Comments

[alexalexes]

В задаче не указано условие, что линии не должны накладываться, возможно только пересечение.
По области знаний задача похожа на "Домики и колодцы".

[havemanyquestions]

Да, спасибо, действительно, забыл указать. Поправил вопрос.

[havemanyquestions]

Так, значит теория графов...
Может, какие-то конкретные алгоритмы?

Answer 1

[Владимир Олохтонов]

Мне кажется, что вот эта статья может вам помочь (проверка графа на планарность): https://ru.m.wikipedia.org/wiki/%D0%9F%D1%80%D0%BE...

Пересечением в вашем случае является совпадение переходов из вершины A в вершину B.

Answer 2

[forspamonly2]

задача в вашей формулировке не имеет решений, кроме вырожденных (когда всё сразу совпадает один к одному).

во-первых, если надо соединять все N элементов, то тупиковых ситуаций с красными линиями никак не избежать, просто потому, что для того, чтобы поменять местами пару линий вам нужно иметь хотя бы одну свободную полосу.

во-вторых, у вас написано: "квадрат", а при одной свободной полосе, в части случаев его не будет хватать по длине. для того, чтобы поменять местами две линии, надо три ячейки в длину: из первой на свободную временную, со второй на первую, и со временной на вторую. так что, в худшем случае (множество линий, которые надо менять местами попарно), это не квадрат, а прямоугольник с соотношением сторон примерно два к трём.

Comments

[havemanyquestions]

Да, уже подумал над тем же. Чтобы получилось соединять группы только при вертикальном или горизонтальном движении, необходимо неизбежно увеличивать этот самый "квадрат" (или по вертикали, или по горизонтали). Ясно из простой модели - две точки с одной стороны, две точки с другой стороны и "соединительный квадрат" из 4 точек. Как раз нужна та самая третья линия, если соединить точки не по прямой. Если добавить диагонали, чтобы избежать использования третьей линии, то решения будут? При использовании того же самого количества соединительных точек в квадрате?