Какая геометрия больше подходит для 3D сферы?

Question

[Vitaliy]

Пробую сделать генерацию сферы с различными уровнями детализации.

Первым была сфера, разбитая по quadtree по ш/д, таки образом получалось слишком большое количество частей на определенную плотность (что уже и говорить о неравномерной плотности геометрии.

Вторая quadtree геометрию на основе куба, но и там по площади треугольники сильно отличаются (на углах они мелкие, на середине большие)

Потом присмотрелся к правильным многогранникам:
из октаэдра также получал отличающиеся по площади треугольники (на полюсах они меньше)


Что касается икосаэдра и додекаэдра - в них визуально не определяются отличия в площади треугольников (но нужно говорить о додекаэдре, в котором грань состоит из 5 треугольников, с вершиной по центру грани)

Все же какой лучше выбрать, и какие еще параметры нужно учитывать, если нужно грани такого многогранника разбивать на относительно равные части, чтобы наладить lovel-of-detail ?

UPD: Икосаэдр, сгенерирован в Blender.

Чем ближе к местам стыка изначальных граней, тем меньше ребра треугольников после разбиения.

UPD:
Понял в чем дело:
представил фигуру в разрезе по горизонтали в центре, где
зеленым - места разреза при соблюдении одинаковой длины ребер, ориентируясь по углу ( то что нужно)
синим - места разреза грани по расстоянию на этой же грани (линейно)
пока не знаю как точно изложить, но результат следующий


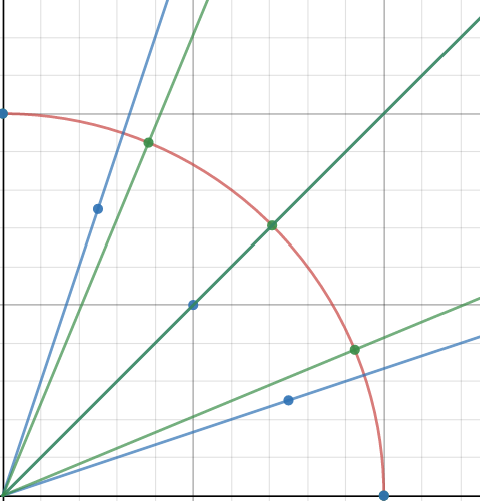
Живой пример: https://www.desmos.com/calculator/plxwk8mukm

Answer 1

[Vitaliy]

В итоге, на примере разбиения октаэдра получил:

UPD: в чем-то получился просчет - площадь при радиальном все же не одинакова (min area: 0.0192 -> max area: 0.0347)
Зеленый (линейный) - стандартный способ разбиения, в нем получается так, что крайние треугольники имеют меньшую площадь. Причем она в 5 раз отличается от максимальной.
Черный - радиальное разбиение, площадь не так сильно отличается сохраняется.
Причина - угловой дефект

Answer 2

[Александр Павлюк]

Для задач LOD вам лучше всего подойдёт сфера из одинаковых равносторонних треугольников.
Но нужно ещё смотреть, что вы хотите наложить на эту сферу, для определённых задач больше подойдёт ваш первый вариант.

Comments

[Vitaliy]

первый хорошо подходит для тайловых текстур, но его геометрия никуда не годится. В лучшем случае, просто подгоню текстуры под геометрию

Answer 3

[GreatRash]

Icosphere - та что справа.

Comments

[Vitaliy]

да, именно это. Там абсолютно все треугольники одинаковы по площади? ( т.к. в октаэдре они не одинаковы)

[GreatRash]

Виталий Столяров: Там все треугольники равносторонние. Этот тип примитива основывается на правильном икосаэдре. Специально был придуман для того, чтобы иметь регулярную сетку.

[Александр Павлюк]

Виталий Столяров: в октаэдре все треугольники одинаковые

[Vitaliy]

GreatRash: кроме него есть еще такие, в которых при увеличении детализации остаются все грани (треугольники) одинаковыми?

[Vitaliy]

Принимая во внимание, что объект должен принимать форму сферы.

[Vitaliy]

Александр Павлюк: проверьте с детализацией = 5
https://threejs.org/docs/?q=oct#Reference/Geometri...

[Александр Павлюк]

Виталий Столяров: с детализацией 5 это уже не октаэдр. У октаэдра 8 граней, потому он и называется так.

[Vitaliy]

Александр Павлюк: имелась в виду геометрия с увеличивающейся детализацией на основе таких многогранников с сохранением относительной площади граней

[Александр Павлюк]

Виталий Столяров: если увеличивать детализацию равномерно (каждую грань бить на одинаковые треугольники), то площадь должна быть одинакова. Вопрос к алгоритму генерации.

[Vitaliy]

Александр Павлюк: в чем критерий равномерного разбиения? Есть пример?

[Александр Павлюк]

Виталий Столяров: Стремиться к одинаковой площади треугольников. Посмотрите как Blender бьет, например. Там похоже, что площадь равная.

[GreatRash]

Виталий Столяров:

кроме него есть еще такие, в которых при увеличении детализации остаются все грани (треугольники) одинаковыми?

Вы чот не туда смотрите. Вот.

[Vitaliy]

Александр Павлюк: проверил, это не так i68.tinypic.com/359d5ab.png

[Vitaliy]

GreatRash: я же и спросил, кроме *Ико* -саэдра есть другие?

[Александр Павлюк]

Виталий Столяров: хмм, действительно. Детальнее икосаэдра нет правильных многогранников на основе треугольников.

[GreatRash]

Виталий Столяров: Бывает ещё сфера из гексов, но это не то, что вам нужно, ибо там встречаются пятиугольники.

Если вам надо 1 в 1 как в блендере. то ссылку я вам дал выше - new THREE.IcosahedronGeometry()

[Vitaliy]

GreatRash: нужно не как в блендере, нужны равные по площади треугольники. Пробовал с додекаэдром, грань представлял как 5 треугольников с вершиной в центре грани. Там, если я не ошибаюсь, при делении точно получатся равные треугольники, но с ним сложнее

[GreatRash]

Виталий Столяров: new THREE.IcosahedronGeometry() - делает сферу с равными по площади треугольниками.

[Vitaliy]

GreatRash: где это можно проверить на достоверность? Например, тем же three.js сгенерировал и получил площади, при детализации = 4 минимальная и максимальная в несколько раз отличаются codepen.io/Ni55aN/pen/QpvOWP?editors=1010

Answer 4

[Александр Скуснов]

Берёте икосаэдр и делаете тесселяцию: вместо одного треугольника будет 4 (при этом все новые и старые вершины продолжают быть вписанными в одну сферу, т.е. имеют одинаковый радиус-вектор). Разбиение продолжается несколько раз. В книге Франка Луны DirectX 12 приведён пример геосферы.

Comments

[Vitaliy]

Все равно треугольники меньше в тех местах, которые ближе к грани (та, что при нулевой детализации грань)

[Vitaliy]

Вот такое нашел phrogz.net/CSS/Geodesics/LinearVersusRadial.gif
Один вариант с linear, второй - radial. И судя по скрину, второй решает проблему с разностью площадей. Но пока не ясно как

[Александр Скуснов]

Треугольники одинаковые. Вы описываете какую-то другую процедуру, не ту, которую я указал.

[Vitaliy]

Александр Скуснов: Пример, codepen.io/Ni55aN/pen/QpvOWP
первый Octahedron
второй Icosahedron, минимальная площадь в 2 раза меньше максимальной.
Или у three.js наверное не совсем корректно вычисляет?

[Vitaliy]

Александр Скуснов: Обновил вопрос, добавив скрин с замерами икосаэдра

[Александр Скуснов]

Виталий Столяров: приложил рисунок (далее код на С). Обратите внимание, что точки m должны получить такой же радиус-вектор, что и исходные точки p, т.е. также лежать на сфере.

[Александр Скуснов]

точнее, там написано, что радиус либо единичный, либо r

[Vitaliy]

Александр Скуснов: это при одном разбиении все треугольники так и остаются одинаковыми, а если таким же образом разбить p1m0m1, то верхний треугольник уже получится меньшего размера

[Vitaliy]

Александр Скуснов: обновил вопрос, добавил пример