Как нарисовать обрамляющую линию вокруг располагающихся рядом фигур?

Question

[seacjs]

У меня имеется поле из неправильных шестиугольников. Каждый из которых закрашивается одним из нескольких цветов.
Каждый из них я рисую по координатам вершин.

Мне необходимо нарисовать линию которая будет обводить все шестиугольники одного цвета, стоящие рядом. В результате должно получится так:

Подскажите алгоритм, с помощью которого можно это реализовать.

Подобное реализовано в разных стратегических играх, например в цивилизации:

Comments

[Даниил Басманов]

Шестиугольники как рисуете?

[seacjs]

Даниил Басманов: Делаю с помощью javascript canvas. У правильных шестиугольников рандомно смещаю центр, затем с помощью d3.js voronoi получаю координаты вершин. Количество многоугольников по x и y одинаково, поэтому легко получаю доступ к соседним многоугольникам.

Answer 1

[ManWithBear]

Вот тут всё хорошо описано https://habrahabr.ru/post/144921/
Множество вершин многоугольников одного цвета составить не проблематично.

UPD. Первое пришедшее в голову решение:
Берем множество всех граней этих шестиугольников. Далее проходимся по нему и удаляем все, которые лежат между шестиугольников одного цвета. В итоге имеем множество граней, необходимых для постройки необходимой фигуры.
Можно даже абстрагироваться от шестиугольников и сделать это для любых фигур.

Comments

[seacjs]

Тут описано для выпуклых фигур. В моем случае получается наоборот.

Answer 2

[Александр]

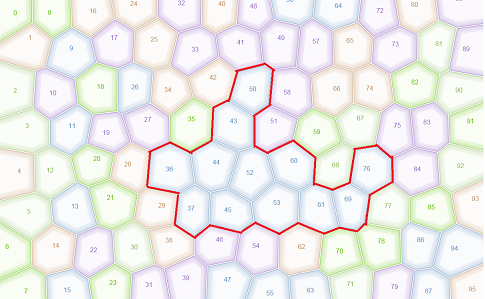
Трудно сказать что-то конкретное, не видя, как именно реализована изнутри структура, описывающая поле.

Предположу, что у вас есть возможность для любой ячейки узнать все шесть её соседей. Если такой метод существует, дальше всё легко.

Примечание: Я буду в ответе использовать термин "множество" в терминологии питона. Если у вас другой язык, воспользуйтесь аналогичной структурой из своего языка. Или используйте простой список, но перед добавлением в него элемента проверяйте, что такого элемента там нет. Иначе цикл никогда не завершится, а список будет разбухать, пока не съест всю память.

Начинаете с одной любой ячейки.

Создайте два пустых множества - назовём их 'currents' и 'visited'.
В currents поместите ту ячейку, с который вы начинаете.

Далее выполняете цикл, пока в currents есть хотя бы одна ячейка:
1. Удалите из currents первую попавшуюся ячейку (далее её я называю "текущей ячейкой").
2. Для этой текущей ячейки найдите всех её соседей.
3. Для каждого соседа:
3.1. Если он того же цвета, что и текущая, и не находится в множестве visited - добавьте его в currents
3.2. Если он другого цвета - проведите границу между этим соседом и текущей ячейкой.
4. Добавьте текущую ячейку в visited
5. Повторять, пока currents не кончится.

Граница нарисована!

Comments

[seacjs]

Вы все правильно заметили, это правильная шестиугольная сетка с слегка сдвинутыми центрами. С помощью вороного получаю координаты вершин многоугольников. Реализовано на js canvas. По вашему алгоритму(немного измененному) я группирую находящиеся рядом многоугольники одного цвета.
Но для отрисовки он не подходит т.к. хотелось бы рисовать непрерывной линией, а не отрезками. Это связано с тем что при отрисовки к фигуре добавляются внутренние тени, а позднее я хотел бы сгладить углы.

Answer 3

[uvelichitel]

Это диаграмма Вороного, если вы смогли ее реализовать на каком нибудь языке, то для вас не должно составлять труда ее раскрасить. На JS такое умеет d3js , вот код модуля.

Comments

[Александр]

Вряд ли это имеет отношение к диаграмме Вороного. Это похоже на обычную правильную шестиугольную сетку, у которой просто слегка рандомно подвинуты вершины. Если присмотреться, то там явно видны горизонтальные и диагональные ряды.

[seacjs]

Да, я как раз и использовал d3.js, но только для того что бы получиться координаты вершин многоугольников. Но для того что бы решить мою задачу, в этой библиотеке я решения не нашел.

Answer 4

[Даниил Басманов]

Медленный, но достаточно простой в реализации алгоритм.

1. Создаёте список связанных шестиугольников одного цвета и выкидываете из него все шестиугольники без соседей другого цвета.
   
2. Создаёте список вершин оставшихся многоугольников
   
3. Создаёте пустую ломаную линию.
   
4. Берёте один многоугольник из списка, ищете у него сторону с соседом другого цвета.
   
5. Двигаетесь по часовой стрелке от этого ребра, выкидываете вершины из списка необработанных и складываете их в ломаную до тех пор, пока не наткнётесь на соседа такого же цвета.
   
6. Переходите на соседа, следующее ребро по часовой стрелке от общего будет внешним. Повторяем 5-6 до тех пор, пока ломаная не замкнётся.
   
7. Если в списке вершин ещё что-то осталось, ищем многоугольники с необработанными вершинами, обходим рёбра по часовой стрелке и создаём ломаные, если встречаются необработанные внешние рёбра.
   
8. Если в итоге получилось несколько многоугольников, значит это многоугольник с дырками. Вершины внешнего контура будут отсортированы по часовой стрелке, а внутреннего - против часовой.
   

Для рисования вам скорее всего понадобится сущность "многоугольник с дырками". В ней должен храниться отдельно большой внешний многоугольник и список многоугольников-дырок. Ломаную можно хранить как отсортированный список вершин. Если рассматривать шестиугольники как регулярную сетку и проиндексировать все вершины, то можно впоследствии достраивать контур при увеличении-уменьшении цветной области.