Как доказать что этот граф планарный, используя две теоремы:
Теорема: Понтрягина - Куратовского.
Граф является плоским (планарным) тогда и только тогда, когда он не содержит подграфа, который гомеоморфен одному из графов Понтрягина - Куратовского.
Теорема: Граф является плоским (планарным), когда он не содержит подграфа, который стягивается к одному из графов Понтрягина-Куратовского.
Я понимаю эти теоремы, но не понимаю, как их использовать для произвольного графа. Не могли бы вы, пожалуйста, натолкнуть на мысль или объяснить, как использовать?
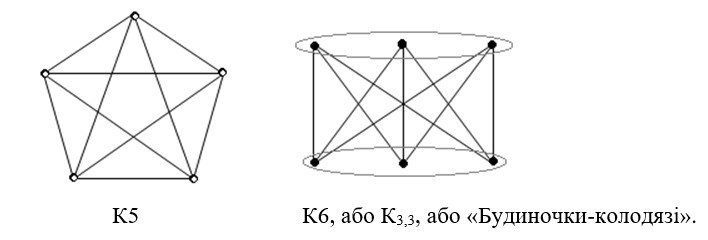
Вот мой граф:
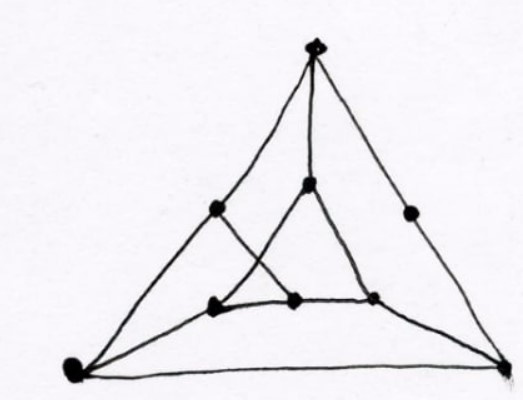
Графы Понтрягина - Куратовского: