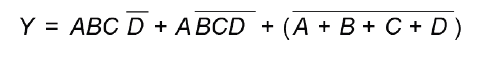Как минимизировать логическое выражение?

Question

[gleendo]

Подскажите какие теоремы нужно использовать и как сократить данное выражение

Answer 1

[Alexandroppolus]

ABC!D + A(!B + !C + !D) + !A!B!C!D

ABC!D + A!B + A!C + A!D + !A!B!C!D

(ABC!D + A!D) + A!B + (A!C + !A!B!C!D)

(ABC + A)!D + A!B + !C(A + !A!B!D)

(A)!D + A!B + !C(A + !B!D)

A!D + A!C + A!B + !B!C!D

A!(BCD) + !B!C!D

больше что-то не сокращается

Comments

[gleendo]

Alexandroppolus А как из этого (ABC + A)!D получилось это (A)!D ?

[Wataru]

iamevg, закон поглощения. Или можно вынести за скобки A, там останется BC+1, что сокращается до 1 и вообще выбрасывается.

Answer 2

[Михаил]

Что-то мне не кажется что эти два выражения равны. Второе выражение будет равно единице если A=0 и любых значениях остальных B, C, D

Но если мы подставим в первое A=0 и любое из B, C, D = 1, то получим 0.

А вообще: создаем таблицу истинности первого выражения (всего 16 строк), переводим в нормальную дизъюнктивную форму, выбрасываем лишние члены. Например, если получилось ABC + !ABC, то это, очевидным образом упрощается до BC.