Как проверить, создают ли линии замкнутую геометрическую фигуру?

Question

[ivandzemianchyk]

И как выбрать из множества фигур наиболее похожую на прямоугольник?

В проекте задача дошла до момента, когда у меня есть множество линий и мне нужно из этого множества выбрать те, которые вместе представляют прямоугольник( или какую-то похожую фигуру нпр. трапез с мерой подобия фигуры на прямоугольник)
Буду благодарен за ответ на любой вопрос:

1. Как проверить замкнутая ли фигура представленная пересечинеим н-того кол-ва линий?
2. Как можно проверить насколько данная фигура похожа на прямоугольник?

буду премного благодарен за любую помощь

Edit:
Работаем на пространстве 2D.
Линия описана двумя точками. Может быть описана любым другим способом.
Линии НЕ парралельни и НЕ перпендикулярны, т.е. идеального прамоугольника не будет

Answer 1

[hazestalker]

Объясню грубо
1. Если линии пересекаются, то нужно найти точки их пересечения. Затем(отталкиваясь от одной точки) проверить пересекаются ли между собой линии пересекающие первые две, принадлежащие нашей точке

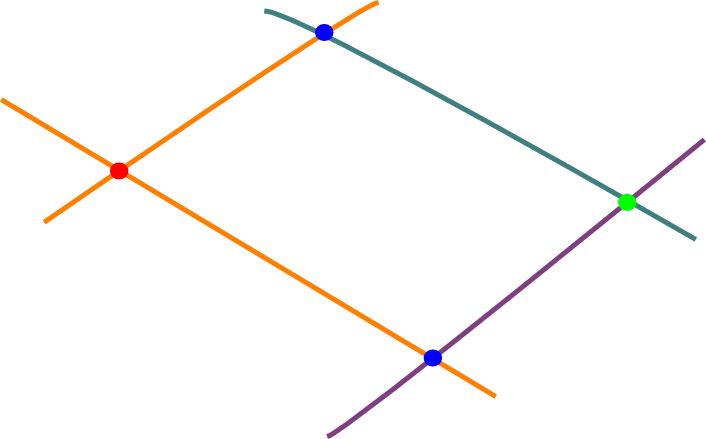
2. Раз у нас есть координаты вершин, мы можем рассчитать углы данной фигуры. Три угла или два противоположных = 90, значит прямоугольник + одинаковая длина рёбер - квадрат
По углам можно любую фигуру определить
Обращайтесь, если нужна помощь)

Answer 2

[Андрей]

По второму вопросу - можно ввести следующие функции :

А) ( (отношение модуля разности диагоналей к их сумме) + (отношение модуля разности одной пары противоположных сторон к их сумме)/2 + (отношение модуля разности пары других противоположных сторон к их сумме)/2 )

Для прямоугольника = "0"
Для параллелограммов нарастает компонента 1
Для трапеций нарастают компоненты 2 и/или 3

Б) Сумму модулей отклонений всех четырех углов от 90 градусов

Answer 3

[AxisPod]

Нечать с того, что определиться бы, что такое линия. Это отрезок, луч или прямая.
Далее следовало бы определиться, в пространстве какой размерности они находятся.
Ну и три, предположим, что плоскость (как следствие обработки изображений), далее предположим, что линии - отрезки исходя из прошлого предположения.

В итоге зная координаты уж очень сложно не понять, пересекаются или нет. Сравнить друг с другом попарно, итого 8 сравнений, определить точки пересечения, и углы и для всего этого, вы не поверите, достаточно школьного курса математики.

Comments

[ivandzemianchyk]

Спасибо за ответ. подправил вопрос, потому что действительно можно было не до конца его понять. Линий будет много, и мы исчем те которые создадут фигуру похожую на квадрат.

[AxisPod]

Ну вот теперь понятнее, ищите пересечения, отсеиваете все отрезки у которых менее 2х пересеченией, должны остаться только те, что образуют фигуру. Останется только в них сделать окончательный отсев и все.

Answer 4

[Михаил Криницкий]

Если под словом "линия" имеется в виду именно бесконечной длины прямая линия, и при этом все линии не параллельны, то не вижу особой проблемы в вопросе №1. Любые две непараллельные прямые обязательно пересекаются. Множество точек попарного пересечения имеющихся прямых обязательно можно пронумеровать, ибо их конечное количество.
Для целей построения многоугольника на этих точках - можно, например, посчитать центр масс всех этих точек пересечения, поставить в него начало полярной системы координат и пронумеровать их против(по) часовой стрелки. Так мы получим последовательность непересекающихся отрезков, составляющих многоугольник. И да, эта ломаная линия будет замкнута. Вопрос совпадения углов для какого-то набора точек решается проверкой, регулирокой точности вычислений или смещением начала полярной СК. Вопрос принадлежности более чем двух точек одной прямой - решается проверками и не имеет принципиального значения.
Правда, гарантировать при всем этом, что полученный многоугольник будет выпуклым - можно только для случая трех прямых.