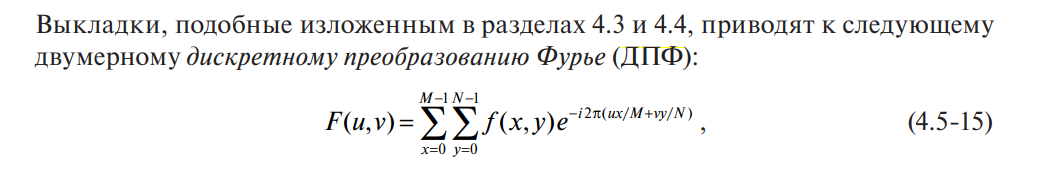Суть вопроса:
Есть бинаризованное черно-белое изображение, полученное после нескольких этапов обработки исходного изображения с помощью методов фильтрации в пространственной области - унифицированая анкета сотрудника - черный печатный текст на белом фоне и черно-белая фотография в углу документа. Так же, в некоторых местах, фон документа имеет артиефакты - "пятна" серого цвета - обласьями пикселей на некооторой части изображения. Артифакты серого цвета могут присутстовать как на чистом фоне, так и служить фоном-подложкой в области текста - т.е в основной своей части - текст на белом фоне, но часть букв,слов может юыть на сером "пятне". Требуется произвести фильтрацию изображения в частотной области.
Предистория и некоторые уточнения (пожалуйста, не пропускайте):
первым этапом частотной фильтрации будет переход в частотную область помощтю ДПФ (знаю, что для адекватных вычислений нужно использовать БПФ, но буду разбираться постипенно). Читал о ДПФ, собственно как и о обработке изображений в книге "Мир цифровой обработки изображений" - С.Гонсалеса, Р.Вудса. Сразу отмечу два момента:
- До этого, я не имел дела с обработкой изображений
- Не знаком с оновами ЦОС
- все "познания" для решения вопроса (в том числе упомянутые методы пространственной фильтрации, которые применялись к исходному изображению), пока что читаю из вышеуказанной книги.
Следует так же отметить, что я знаю о том что есть готовые библиотеки для БПФ и ДПФ, как раз одну из них, после долгих неудачных попыток реалезации ДПФ "руками" - использовал - библиотека AForge.Imaging (
www.aforgenet.com/aforge/framework - сайт фреймворка.) Юиблиотека со своими задачами справляется, но я получаю только изображение фурье-спектра, мне же нужны преобразованые значения точек (пикселей изображения) для частотной области - для последующего их использования. Итого, почему данная библиотека мне не совсем подходит:
- Библиотека дает на выходе только Фурье-спектр в виде изображения, без возможности использовать "сырые данные" преобразования из пространственной в чатотную область
- Библиотека является "черным" ящиком, что лишает возможности экспериментов с целью "покрутить и посмотреть, что да как" (мне как новичку во всем этом - это действительно нужно - никто не говорит постоянно писать велосипеды, но разобраться в новой для себя области работы - необходимо)
- по поводу претензии №2 - в далнейшем, мне будет необходим производить гомоморфную фильтрацию, где в ДПФ нужно передавать ln от значения пикселя или же апроизводить ДПФ над всем изображением после полной яркостной логорифмической фильтрации, но хотелось бы иметь возможность написать функцию ДПФ, позволяющую передавать не только все изображение, но и и передавать отделные пиксели.
Суть проблемы:
Для того, что бы разобраться с двумерным случаем - начал с чего попроще - с одномерного ДПФ для волны (звуковой или еще какой), нашел два вот таких примера:
/////////ДПФ
double Re = 0, Im = 0, summaRe = 0, summaIm = 0, Ak[512] = {0}, Ak_1[512] = {0}, Arg = 0;
for (int i = 0; i < 512; i++){
summaRe = 0; summaIm = 0;
for (int j = 0; j < 512; j++){
Arg = 2.0*M_PI*j*i/512.0;
Re = cos(Arg)*(massiv[j]);
Im = sin(Arg)*(massiv[j]);
summaRe = summaRe + Re;
summaIm = summaIm + Im;}
Ak[i] = sqrt(summaRe*summaRe + summaIm*summaIm);}
512 отсчетов заданно по условию изначального вопроса - я же замени его, допустим на ширину изображения (если представить изображение, как еденичную полосу (вектор) пикселей). Как я понимаю, согласно вот этой формуле из книги:
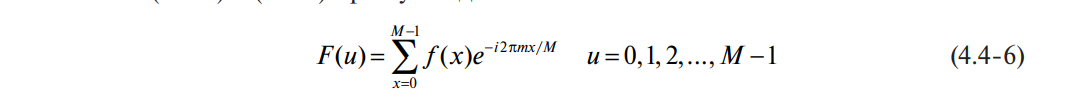
для одномерного случая ДПФ - два цикла - один для отсчета точек самого преобразования и один - для суммы значений по каждой точке.
Так же, мне в принципе понятно, откуда беруться синусы и косинусы (да,я знаю, что ДПФ - по сути разложение сигнала на гормоники, но я скорее про математическую запись):

Еще один найденный пример, на C#:
public class FurieTrans {
public List<Complex> koeffs;
public double K;
public FurieTrans() {
koeffs = new List<Complex>(); }
public void dpf(List<Point> points, int count) {
koeffs.Clear();
K = points.Count;
//Цикл вычисления коэффициентов
for(int u=0; u<count; u++)
{ //цикл суммы
Complex summa = new Complex();
for (int k = 0; k < K; k++) {
Complex S = new Complex(points[k].X, points[k].Y);
double koeff = -2 * Math.PI * u * k / K;
Complex e = new Complex(Math.Cos(koeff), Math.Sin(koeff));
summa += (S * e); }
koeffs.Add(summa/K); } }
public List<Complex> undpf() {
List<Complex> res = new List<Complex>();
for(int k=0; k<K-1; k++) {
Complex summa = new Complex();
for (int u = 0; u < koeffs.Count; u++ ) {
double koeff = 2 * Math.PI * u * k / K;
Complex e = new Complex(Math.Cos(koeff), Math.Sin(koeff));
summa+=(koeffs[u]*e); }
res.Add(summa); }
return res; } }
Теперь, на основе всего этого и формулы из книги для двумерного случия ДПФ:
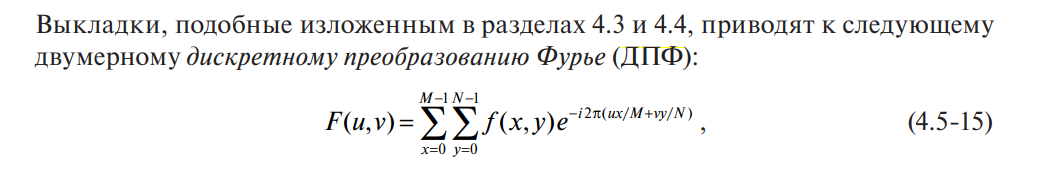
- вот, что получилось у меня:
static void MakeFurieTransform(FT_mode mode) {
Bitmap FFT_bitmap = new Bitmap(workBitmap.Width, workBitmap.Height);
double realPart = 0, imagePart = 0, rotAngle = 0, amplitude = 0;
double e = 0;
double summ = 0;
if (mode == FT_mode.direct) {
for (int u = 0; u < workBitmap.Width; u++) {
for (int v = 0; v < workBitmap.Height; v++) {
summ = 0;
//циклы суммы
for (int x = 0; x < workBitmap.Width; x++) {
for (int y = 0; y < workBitmap.Height; y++) {
double Rot_coefficient = -2 * Math.PI * (u * x / workBitmap.Width + v * y / workBitmap.Height);
realPart = Math.Cos(Rot_coefficient);
imagePart = Math.Sin(Rot_coefficient);
e = realPart + imagePart;
summ += workBitmap.GetPixel(x, y).ToArgb() * e; } }
//формируем Фурье-спектр
amplitude = Math.Sqrt(realPart * realPart + imagePart * imagePart);
rotAngle = Math.Atan(imagePart/realPart);
int_R = (int)amplitude;
NormalizePixel(ref int_R);
FFT_bitmap.SetPixel(u, v, Color.FromArgb(int_R, int_R, int_R)); } } }}
Собственно, сам вопрос:
- Там, где я получаю значение е -
e = realPart + imagePart; - что делать с комплексной частью i возле синуса? Т.е. e^iAngle=cos(Angle)+ i sin(Angle) - что делать с мнимой частью при реалезации?
- Вот здесь:
amplitude = Math.Sqrt(realPart * realPart + imagePart * imagePart);
rotAngle = Math.Atan(imagePart/realPart);
int_R = (int)amplitude;
NormalizePixel(ref int_R);
FFT_bitmap.SetPixel(u, v, Color.FromArgb(int_R, int_R, int_R));
- я не совсем понимаю, что должно служить новыс значением цвета пикселя. Правильно ли я делаю?
P.S.
Использованные источники:
Пример кода №1 -
https://www.cyberforum.ru/cpp-builder/thread860204.html
Пример кода №2 -
https://www.cyberforum.ru/digital-signal-processin...
Что читал, помимо книги:
https://habr.com/ru/company/otus/blog/449996/
psi-logic.narod.ru/fft/fft.htm (не все из оглавления - только первые разделы с теорией)
Некоторые вопросы, которые могут возникнуть:
1.Примеры исходных изображений/полученного спектра? - нет, к сожадению не могу выложить (спектр не могу выложить - т.к по нему можно восстановить исходное изображение)
2.Зачем "вот это все" ? - 1. Я учусь, как и все. Поэтому, бегу в стог с граблями. 2.Фмнальная цель "вот этого всего" - подготовка иходного изображения (довольно специфичного) к OCR.
3.Почему c#, а не например С++? - немного знаю C#, поэтому выбор пал на него;легче читать/ писать
при обучении в новой области, что позволяет сконцентрироваться на теоретической проблеме, а не на отслеживании памяти - как в С++(субъективно) (да-да, плохому программисту рапределение памяти мешает) + легче подрубить тот же Tesseract OCR (тоже субъективно).
4.Почему работа с изображениями, частично ЦОС, и прикостыливание к этому OCR, а не например нейронные сети или *подтавьте свой вариант*? - не знаю, вот честно, не знаю. Не работал до этого ни с изображениями, ни с нейронками, поэтому, решил пойти как-то вот таким "классическим" путем обработки изображений с помощью фильтров.
5.Может все это не надо и делать упор на разные библиотек OCR? - может быть, но я пробовал подавать исходное изображение на вход, как для Tesseract OCR, так и для IronOCR - результат, скажем прямо - печальный.