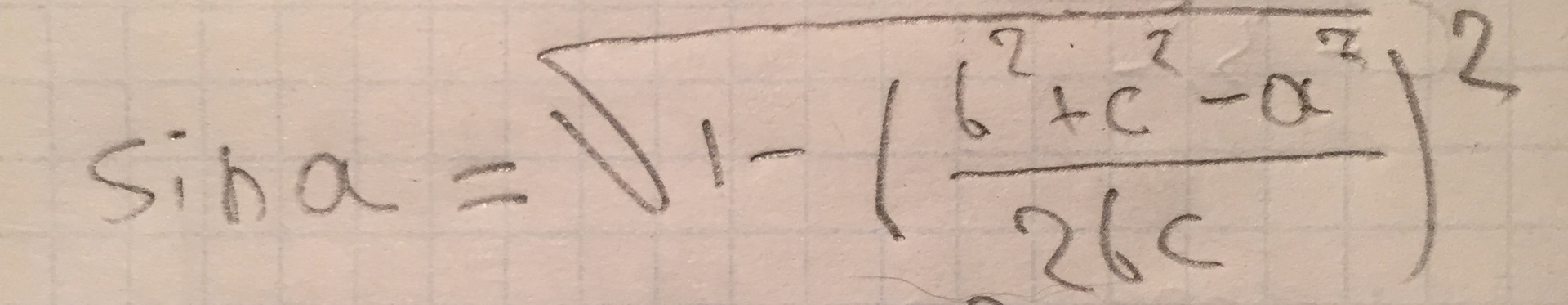Почему основное тригонометрическое тождество работает всегда?

Question

[Dmitriy Grape]

В 8 классе мы проходили основы тригонометрии, сейчас я в 9, и у меня появился такой вопрос: как найти синус, косинус и тангенс у произвольного непрямоугольного треугольника, я воспользовался теоремой

Квадрат каждой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними

Отсюда я легко вывел формулу косинуса, окей, а как найти синус? Я вспомнил про Основное Тригонометрическое Тождество (Далее: ОТТ).

Я загуглил, корректно ли его использовать в данном случае. Да, всё окей, получилось вот:
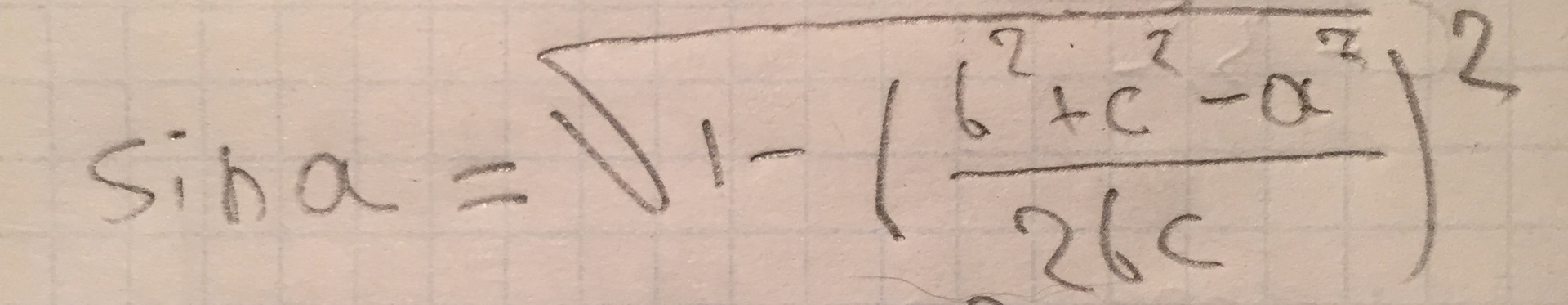
(Конечно, можно раскрыть скобки, но тогда формула будет некрасивой и длинной)

Но теперь я задумался: а почему тут работает ОТТ, если оно доказывается с помощью теоремы Пифагора?

Answer 1

[Wataru]

> а почему тут работает ОТТ, если оно доказывается с помощью теоремы Пифагора?

От того, в каком порядке вы применяете доказанные теоремы, их истинность не меняется. ОТТ - доказано для любого значения угла. Все, независимо от того, в треугольнике ли вы чего-то считаете или матрицу поворота плоскости на заданный угол, или считаете площадь вашего куска пирога.

ОТТ применимо всегда! Для любых аргументов. Но, возможно вас именно это и запутало, после применения ОТТ и взятия корня, по идее, у вас получится +-sqrt(...). Потому что x^2=9 => x=3 или -3. Два варианта извлечения корня, 2 варианта для синуса.

Но, поскольку вы знаете, что угол в треугольнике не может превышать 180 градусов, вы знаете, что синус этого угла всегда неотрицательный. Поэтому -sqrt() можно отбросить как лишнее значение и получить вашу формулу. В формальном доказательстве эти рассуждения надо учитывать.