Всем привет! Участвую в одном из курсов Яндекса и есть одно из следующих заданий:
Реализовать алгоритм нахождения ближайшего соседа, где у каждого из ребер имеется 2 и более параметров
В качестве алгоритма нахождение ближайшего соседа использую
алгоритм Дэйкстры
Входные параметры следующие:
const routs = {
start: { a: 10, finish: 20, c: 9 },
a: { b: 5 },
b: { finish: 0.5 },
c: { b: 35 },
finish: {},
}
итог:
{ distance: 15.5, path: [ 'start', 'a', 'b', 'finish' ] }
С этими входными данными он справляется отлично, вопрос в реализации алгоритма для множества параметров.
Если к каждой из точек(значение рёбер) добавится ещё n-параметров, алгоритм будет эфективным в данном случае или есть другие реализации/алгоритмы ?
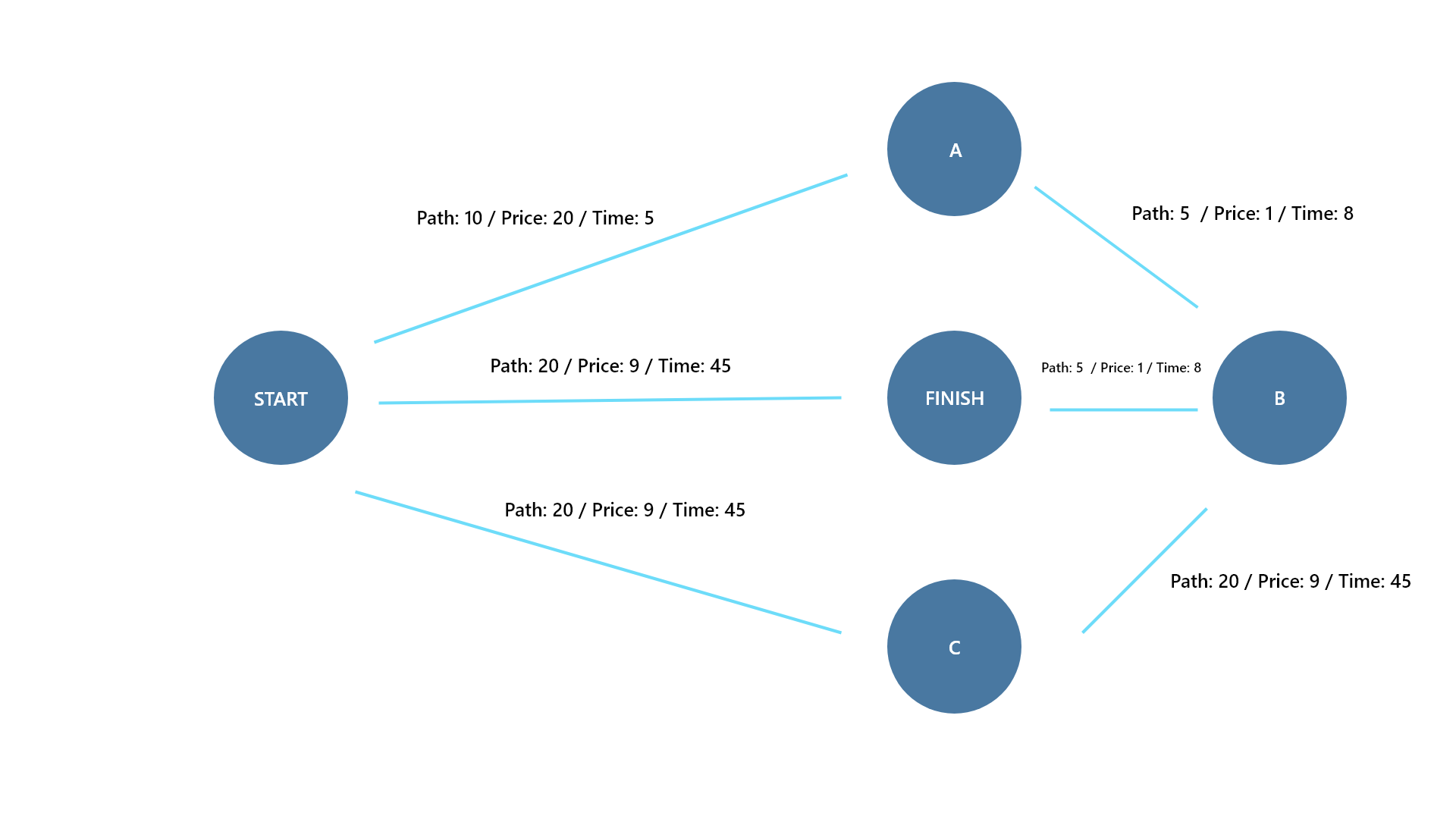
Входные данные с множеством параметров:
const routs = {
start: {
a: { path: 10, price: 20, time: 5 },
finish: { path: 20, price: 9, time: 45 },
c: { path: 9, price: 8, time: 12 },
},
a: {
b: { path: 5, price: 1, time: 8 },
},
b: {
finish: { path: 0.5, price: 0.2, time: 2 },
},
c: { b: { path: 35, price: 35, time: 1 } },
finish: {},
}
Теперь, помимо path добавилась цена(price) и время ожидания такси(time).
В теперешней моей реализации алгоритм высчитывает только по одному параметру, для вычесления со множеством параметров данный алгоритм подходит или есть более лучшее решение ?
