Как выразить переменную из диффиренцильного уравнения?

Question

[bobs32]

Если решать такую задачу в маткаде, выходит следующее:

При попытке получить такой результат на питоне выходит ошибка.

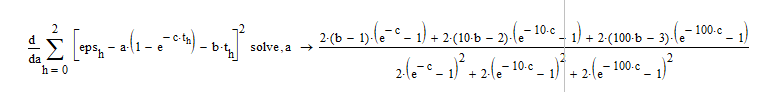
from sympy import *
import numpy as np
x, c, a, b = symbols('x y a b')
n=0
f= symbols('f', cls=Function)

eps = ['1', '2', '3']
t = ['10', '100', '100']

f=summation((int(eps[n])-a*(1-exp(-c*int(t[n])))-b*int(t[n]))**2, (n, 1, 2))
   
print(dsolve(f(x).diff(a), a))

В чем может быть проблема?
Обязательно решить эту задачу на питоне по причине того, что маткад не справляется, если n>3

Answer 1

[Руслан .]

Тут вроде и в уме решается не очень сложно.
1. Раскрываем скобки - возводим в квадрат.
2. Берем производную "d/da" от полученного - все члены не содержащие "a" при этом исключаются, т.к. производная от константы равна нулю.
3. выражение 1-exp(-c*t(i)) можно вынести за скобки, в итоге:
Пусть R(i) = 1-exp(-c*t(i))
sum[(-eps(i) + 2*a*R(i) + b*t(i))*R(i)]

Дальше выражаем "a":
sum[(2*a*R(i)*R(i)] = sum[(eps(i) - b*t(i))*R(i)]

В итоге:
a = sum[(eps(i) - b*t(i))*R(i)]/sum[(2*R(i)^2]

если я со скобками нигде не накосячил.

P. S. У вас в питоновой версии список t не совпадает с маткадовой версией, если верить маткаду, то
t = [1, 10, 100]

Comments

[bobs32]

Спасибо за ответ!
Да, я понимаю, легче это решить руками, но после выражения А будут еще дальнейшиие операции, так что хотелость бы чтоб это делалаось автоматически