Какая есть литература, алгоритм для расположения минимального количества дозорных башен для охраны территории на плоскости?

Question

[Вадим Мамонов]

Есть следующая задача:
Задано некоторое ограниченное многосвязное множество А, необходимо расставить минимальное количество дозорных вышек, с углом обзора 360 градусов и с бесконечным радиусом видимости, так, чтобы совместная область обзора дозорных вышек равнялась множеству А.

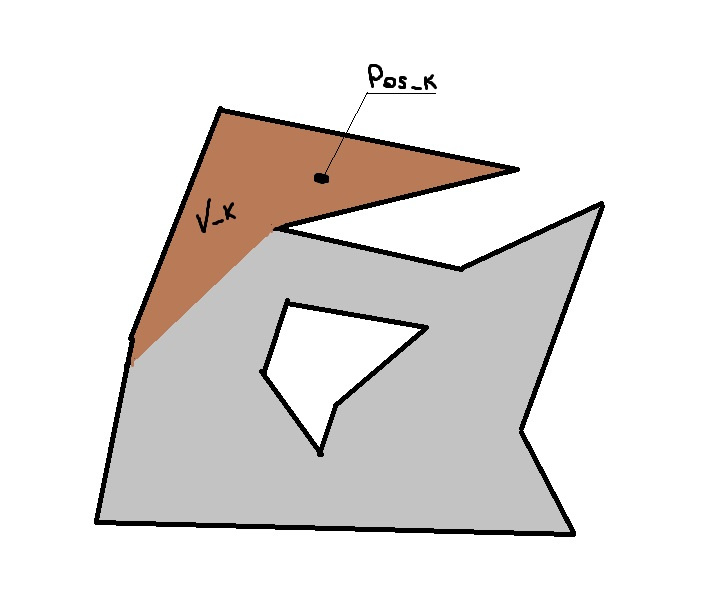
Пример А:


Пример вышки и её области видимости:


Текущая формализация:
A - ограниченное многосвязное множество из R^2 ( охраняемая территория )

N - натуральное число ( количество дозорных вышек )
Pos_k - точка из A ( позиция k-ой вышки )
V_k - подмножество из А, звездная область относительно точки Pos_k ( область видимости k-ой вышки )

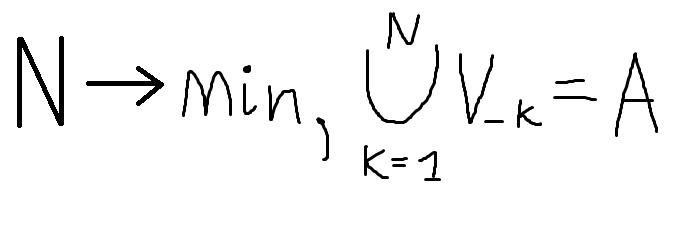На данный момент, я придумал жадный алгоритм:
N = 0.
Пока A != ПУСТО делаем
---Находим позицию для вышки так, чтобы её область видимости была максимальна. (На A ввожу сетку, для ---каждого узла сетки нахожу площадь области видимости из данного узла, далее выбираю узел с ----максимальной площадью) Так и получаем позицию вышки.
---Далее из A удаляем область видимости, получившейся вышки, N++;

Но, не понятно будет ли он оптимальным?(
Возможно, его оптимальность можно доказать из теоремы Радо-Эдмондса
Но, если не получится это доказать, то хотелось бы найти не жадный алгоритм.

Подскажите, какую литературу можно почитать?
Или может есть похожая задачка?
А может динамическое программирование тут применить? (не знаю к месту ли это, но дин. прогр. я не очень знаю)

Comments

[devalone]

Задано некоторое ограниченное многосвязное множество А

Что это значит? Как конкретно задана территория?

[АртемЪ]

Но, не понятно будет ли он оптимальным?(

Какой критерий оптимальности?
Оптимально это найти приемлемое решение с минимумом затрат, или найти решение максимально приближенное к идеалу, не взирая на затраты?

Answer 1

[longclaps]

Задано некоторое ограниченное множество

Такая терминология в геометрической задаче выдаёт некоторую вашу беспомощность. Попробуйте вернуться к Началам Эвклида, у него всё поприличнее.
Жадный алгоритм вы возможно и придумали, но раскрыть не пожелали. Ключевой вопрос: какою мерой будете мерять область видимости?

Comments

[Вадим Мамонов]

На счет ограниченное множество, для меня это означает, что можно это множество в окружность конечного радиуса заключить.

Какою мерой будете мерять область видимости?
Хотел взять обычную площадь.

Жадный алгоритм вы возможно и придумали, но раскрыть не пожелали.
Я, вроде, написал про него.
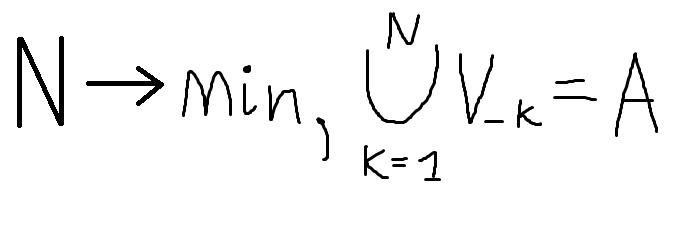На данный момент, я придумал жадный алгоритм:
N = 0.
Пока A != ПУСТО делаем
---Находим позицию для вышки так, чтобы её область видимости была максимальна. (На A ввожу сетку, для ---каждого узла сетки нахожу площадь области видимости из данного узла, далее выбираю узел с ----максимальной площадью) Так и получаем позицию вышки.
---Далее из A удаляем область видимости, получившейся вышки, N++;

[longclaps]

Вадим Анисов, смотри: твоя проблема не в том, чтобы замести площадь по-максимуму, а в том, чтобы не осталось неосвещенных закоулков. Естественная метрика здесь - количество вершин, до которых добивает башня - по крайней мере для односвязной области. Для дырявой это не годится.

[Вадим Мамонов]

Ваша метрика - это количество начал, концов линий до которых добивает башня?
Вот я их на примере отметил
Для дырявой это не годится.
А к чему относится дырявая? К тому, что видит вышка? Или ко всей охраняемой территории?

Охраняемая территория - это многосвязное множество.
А область видимости вышки, это односвязное множество.

[longclaps]

Вадим Анисов, дырявая - это как бублик, вот дырка от бублика может затенять обзор.
Да, метрикой могло бы быть количество закоулков, до которых добивает башня.
Я думаю, может быть полезна такая эвристика: Расставлять точки, из которых не видно друг друга (вот это будет как раз жадный алгоритм). А после расставлять башни, которыенакроют эти точки.
Идея в том, что таких взаимно слепых точек будет гораздо меньше, чем вершин многоугольника.

[Вадим Мамонов]

Предлагаете расставлять точки на границе территории так:
Сначала ставим точку так, чтобы она добивала до большего количество начал, концов линий ( или самую большую площадь покрыла, по принципу дозорной башни )? Далее точно также ставим новую точку, чтобы она не видела старые..

Теперь расставляем вышки, так чтобы все такие точки были видны. Тоже жадиной?

[longclaps]

Вадим Анисов, еще проще: начинаешь с любой вершины и идешь вдоль границ по часовой, пока видимость не нарушится. Добавляешь точку в набор.

[sim3x]

По-моему расставить не проблема - можно и ГА натравить
Как доказать оптимальность расстановки?

[longclaps]

sim3x, никак. Интуитивно кажется, что задача о распределении контроля над "глухими закоулками" разным башням эквивалентна задаче коммивожера. Замечу, что исходная задача выглядит сложнее - там нужно контролировать не дискретные закоулки, а всё.

[sim3x]

longclaps, очевидно, что должна существовать теория покрытия невыпуклыми многоугольниками

Мне трудно представить как сюда можно всунуть коммивояжера

[longclaps]

sim3x, хех, задачи нерегулярного замощения - есть такая тема. До теории не дотягивает - так, отрывочные результаты.

[sim3x]

longclaps, лучше, чем ЗКП

В данном случае, скорее стоит прояснить с преподом, что вообще требуется от "доказательства"

[Вадим Мамонов]

Спасибо большое.

Надо всё это протестировать. Отпишусь, как только сделаю это.

Вот пример, я взял красную, желтую и оранжевую вершины. ( это наше подмножество точек B )

Далее начинаю жадно расставлять вышки Здесь нельзя так расположить вышку, чтобы 3 точки попали в обзор, максимум 2.
На рисунке я обозначил синим цветом множество, куда можно поставить вышку, чтобы она видела 2 точки (максимальное количество точек )

В 3 множество точно нельзя ставить, т.к. нужно будет 3 вышки, чтобы покрыть все.
А в 1 и 2 множестве есть позиции, их я обозначил зелёным цветом, которые позволяют поставить 2 вышки) и что позволит увидеть все, но чтобы получить зеленное множество, я использовал жадность внутри синих множеств.


Может так и поступить.
Сначала строю это подмножество B.
Далее жадностью определяю синее множество, относительно точек из B.
Далее жадностью ищу в нем зелёное множество.

[longclaps]

Вадим Анисов, еще раз проговорю без рисунка.
Берёшь тупо все вершины со всех границ - внутренних, внешних - неважно.
Из каждой выпускаешь лучи во весь сектор угла с этой вершиной.
Эти сектора (некоторые из них) будут пересекаться. Это значит, что область пересечения просматривается из всех причастных секторов, и, наоборот, из этой области просматриваются все причастные закоулки.
Берешь зону, где перекрываются максимальное число секторов (жадный, ага), ставишь башню.
Ищешь следующую зону, покрывающую максимум непокрытых секторов.

Answer 2

[Вадим Мамонов]

Если кому еще интересно, то чтобы точное решение найти, можно данную задачу свести к задаче о минимальном покрытии множества.

Answer 3

[Віктор Короп]

Если видимость каждой вышки максимально, то мне кажется, что это и будет оптимальный вариант, но доказать это я не могу(

Answer 4

[Philipp]

Итак, обычно сторожевые башни размещают на внешней стороне охранямого периметра. Это позволяет осматривать территорию как изнутри (внутренее покрытие), так и снаружи (внешнее покрытие).
Правильными критериями оптимальности при постановке задачи должны быть следующие:
1. Полное внутреннее покрытие
2. Минимальное внутреннее перекрытие
3. Максимальное внешнее покрытие
4. Радиус видимости человека в ночное время и при обычной непогоде (например средний снегопад или дождь).
5. Минимальное количество точек

Думаю надо начинать отсюда stu.sernam.ru/book_plane.php?id=25
Потом читать про нелинейное программирование и градиентный спуск.

Comments

[Вадим Мамонов]

Спасибо большое, с помощью вашей наводки вышел на точное решение. Ноо в другой книжке.

Это задачу можно свести к задачи о минимальной покрытии. Т.е. целочисленное программирование.

Answer 5

[profesor08]

Ставишь в одну точку и смотришь сколько покрывает, ставишь в следующую и тд. Выбираешь из всех результатов один с максимальным покрытием. Далее для непокрытых участков повторяешь то-же самое. Идеальный вариант решения для твоей задачи из примера это две вышки. На крутой алгоритм это не похоже, но даст тебе понять как решать эту задачу. Собственно иллюстрация:

Answer 6

[Андрей Малаев]

Я бы ставил башни в углы. Так как перебор всех вариантов слишком долгий то проще было бы ставить именно в углы при этом нужно понимать, что для одного отрезка нет смысла ставить башню в оба угла

Comments

[Сергей Соколов]

Fail:


В центре достаточно одной башни на всю звезду. Если ставить по углам, понадобится больше, чем 1 башня. Напр. башня в A не попадает в луч D.