Как реализовать точный алгоритм правильной раскраски рёбер графа?

Question

[VerNika]

Нужно найти хроматический индекс графа. Пока реализовала только неточный алгоритм путем поиска степеней вершин графа, последовательного выбора вершины с максимальной степенью и раскраски инцидентных рёбер выбранной вершины в разные цвета, пока есть ещё неокрашенные.

На то он и не точный, что выдаёт только максимально приближенный хроматический индекс.
Вот пример его ошибки, раскрашивает 5-ю цветами:

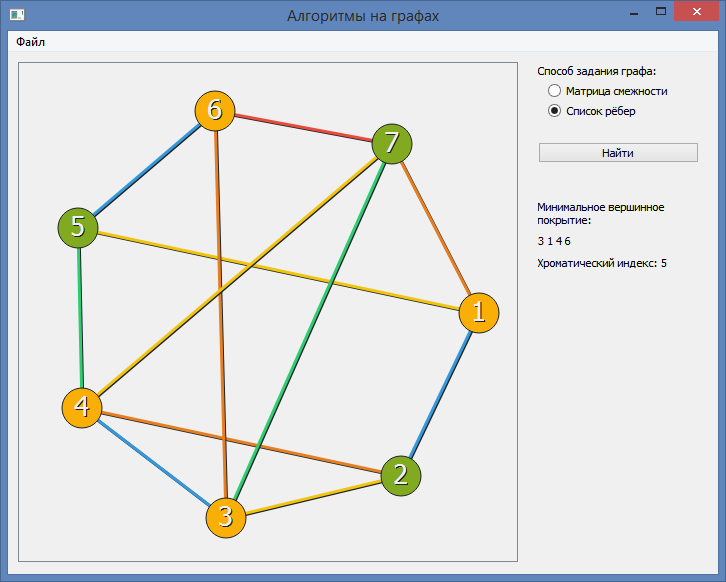
Хотя можно 4-мя:


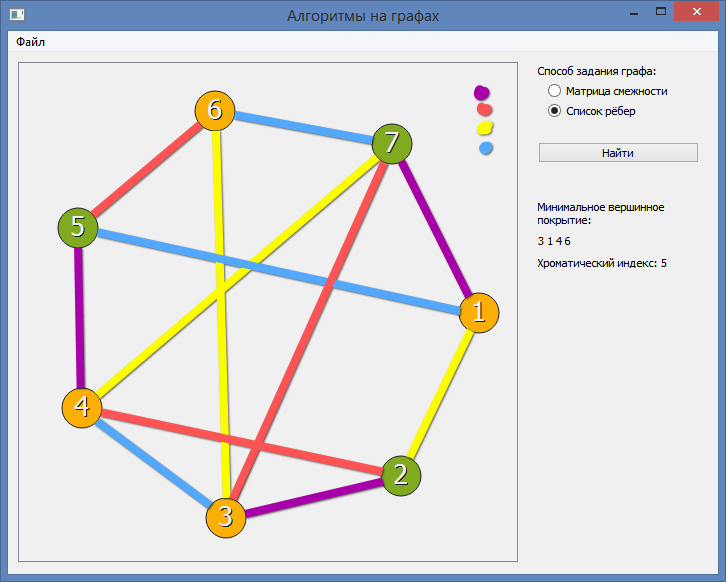
Как реализовать точный алгоритм правильной раскраски рёбер графа? Бить в лоб перебором всех окрасок - не вариант. Нужно что-то побыстрей и алгоритмичней. У самой идей нет, вернее были, но они тоже являются неточными. Пробовала гуглить, для раскраски ребёр ничего нормального не находила, только для раскраски вершин.

Answer 1

[nirvimel]

Существуют алгоритмы полиномиального времени, создающие оптимальную раскраску двудольных графов и раскраску простого не двудольного графа с числом цветов {\Delta}+1.

Однако, в общем случае, задача поиска оптимальной рёберной раскраски NP-полна и самый быстрый из известных алгоритмов для неё работает за экспоненциальное время.

Рёберная раскраска

Итак, можно найти раскраску в Delta + 1 цветов за полиномиальное время (что тоже может оказаться совсем не быстро). Но чтобы доказать, что не существует раскраски (иначе, найти ее) ровно в Delta цветов, необходимо решить NP-полную задачу за экспоненциальное время.
(Delta - максимальная степень вершины).

Comments

[VerNika]

Мне нужен алгоритм. Понятно дело, что для такой задачи быстрых нет, но мне нужен, чтобы хотя бы не методом полного перебора находился результат.

[nirvimel]

VerNika:

Бить в лоб перебором всех окрасок - не вариант.

Суть вышесказанного в том, что это - как раз и есть единственный вариант. И никакого принципиально иного (более быстрого) варианта не может существовать.
Программный код можно, конечно, оптимизировать, но это даст только линейное ускорение во сколько-то раз по сравнению с неоптимизированным оригиналом. Превратить экспоненциальную сложность алгоритма (зависимость времени выполнения от количества вершин) в линейную - невозможно.

[VerNika]

Просто я в этом не особо шарю, надо поразбираться. Ну что же, перебором, так перебором. Тогда, я так понимаю, из теоремы Визинга находим возможные минимальные индексы, и потом тупо перебором от наименьшего?

[nirvimel]

VerNika: Алгоритмы раскраски, например.

[VerNika]

nirvimel: Благодарю!

[VerNika]

nirvimel: Это нормально, что он находит раскраску для относительно небольшого графа, который указан в верху, за минут этак 5?