Я хочу построить регрессию с несколькими переменными (multiple features). В моих данных у меня n = 23 переменных и m = 13000 тренировочных примеров. Вот график моих тренировочных данных (площадь квартиры vs цена):
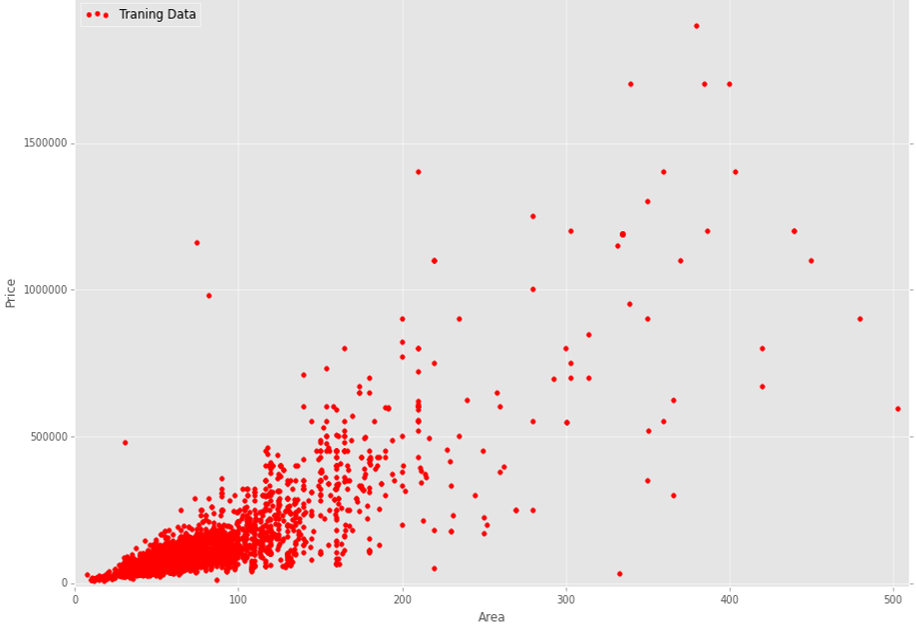
Здесь на графике отображены 13000 тренировочных данных. Как вы можете видеть, это достаточно шумные данные. Мой вопрос: какой алгоритм регрессии больше подходит и обоснован для использования в моем случае. Имею ввиду логично ли использовать простую линейную регрессию или лучше использовать какой-либо нелинейный алгоритм регрессии.
Для наглядности приведу примеры. Вот отвлеченный пример линейной регрессии:
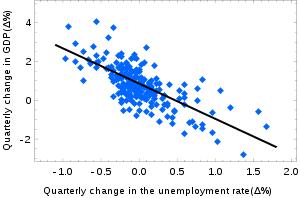
А также отвлеченный пример нелинейной регрессии:
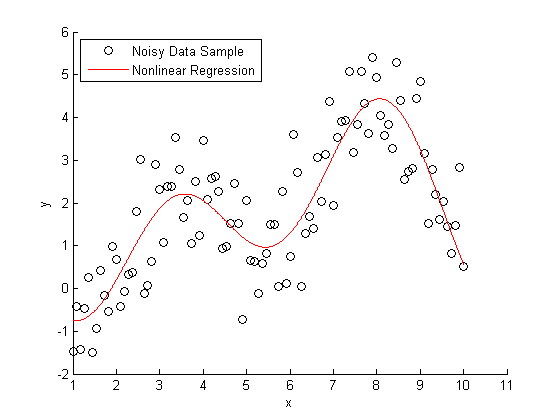
А вот примеры с гипотетическими линиями регрессии для моих данных:
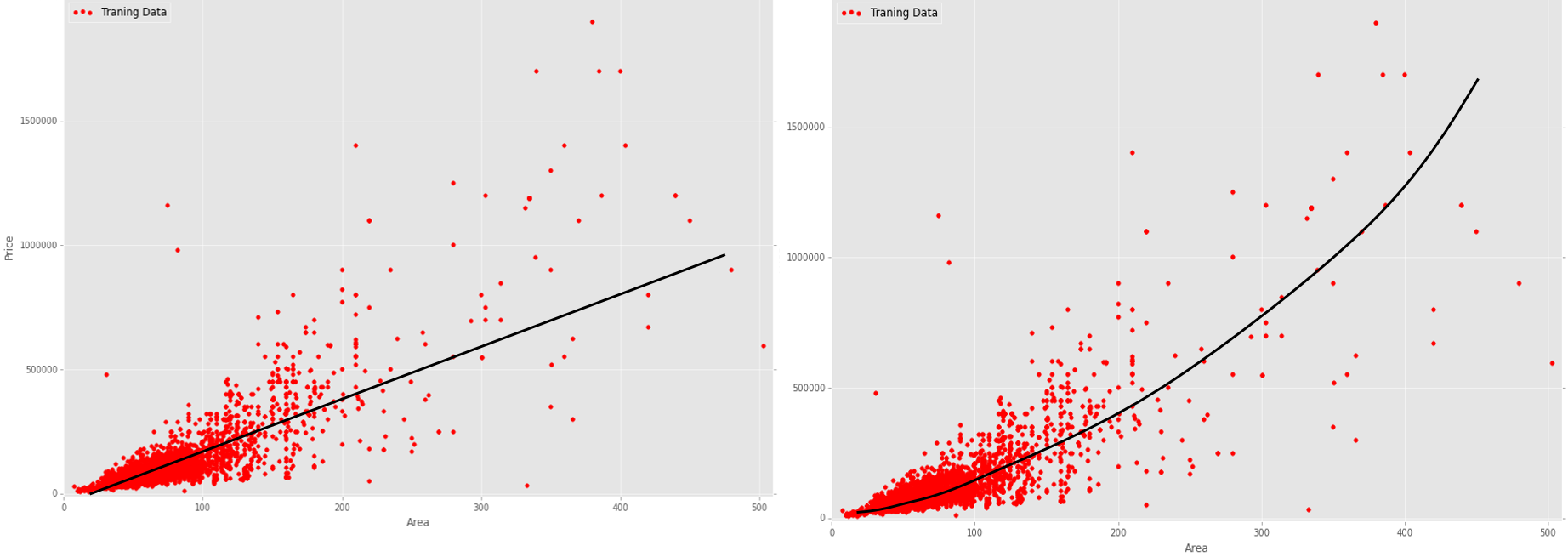
Насколько я понимаю, примитивная линейная регрессия для моих данных произведет большую суммарную погрешность (error cost), так как эти данные шумные и разбросанные. С другой стороны, здесь также не прослеживается какой-либо отчетливой нелинейной зависимости (например синусоидальной). Какой алгоритм регрессии более рационально использовать в моем случае (цены на квартиры) для того чтобы получить более точное прогнозирование цен. И почему этот алгоритм (линейный или нелинейный) более рационален?
Дополнение:
Вот так выглядит мой график линейной зависимости цены от всех 23 параметров , отображенный на данных цена-площадь:
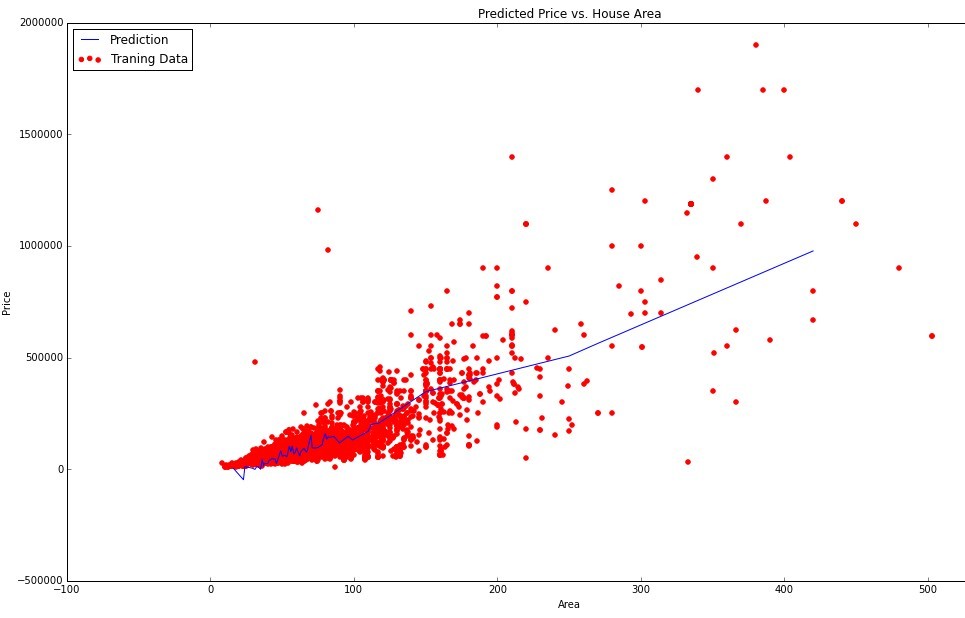
Я не знаю, как бы выглядела НЕлинейная зависимость в таком случае. И была бы она более рациональна чем линейная.




